
Chapter 12: Sources of Magnetic Fields
12.0. Overview
Let's get started!
12.1. Currents Produce a Magnetic Field
Up to this point we've looked at the magnetic fields as a property of magnets, or of the earth itself. Now let's turn our attention to how electric currents can produce a magnetic field.
12.1.1. Oersted
In 1820, Hans Christian Oersted discovered that moving charges produce a magnetic field. The direction of the field is determined using a RHR.
Direction of magnetic field around a wire
If a straight wire is grasped with the right hand with the thumb in the direction of conventional current flow, the fingers curl around the wire in the direction of the magnetic field.
The magnitude of the magnetic field B is the same everywhere on a circular path perpendicular to the wire and centered on it. Experiments reveal that B is proportional to I, and inversely proportional to the distance from the wire.
12.1.2. The Biot-Savart Law
To determine the magnitude of the magnetic field in the vicinity of a current-carrying wire, one strategy is the Biot-Savart Law.
Magnitude of a magnetic field near a wire
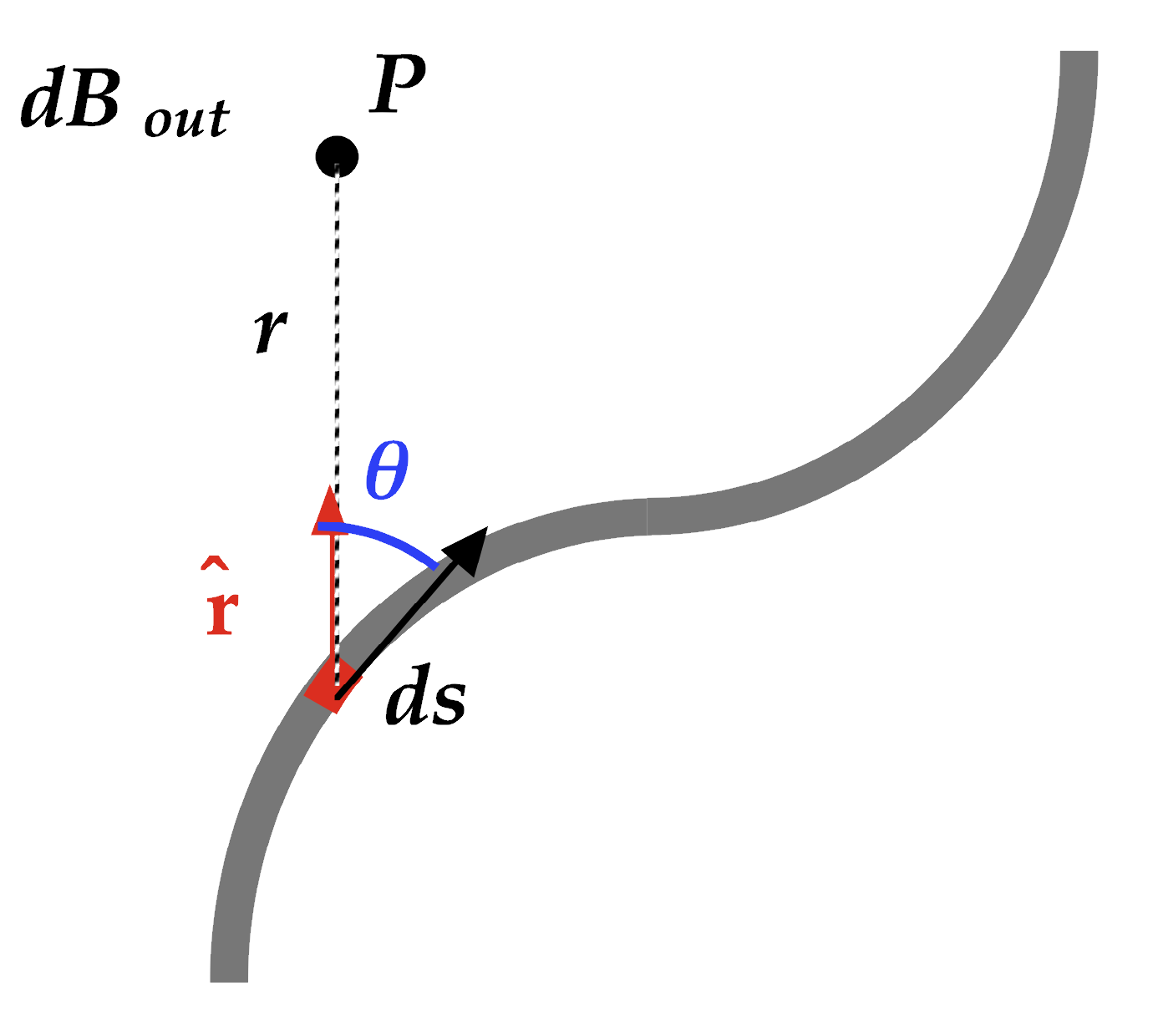
The Biot-Savart Law describes the magnetic field dB due to a length of wire carrying a current as follows:
In this equation:
- dB is the magnetic field at a point P perpendicular to the segment of wire ds and perpendiular to the unit vector r from ds to P.
- I is a steady current in the direction of ds.
- ds is a small segment of wire
- "hat-r" is a unit vector there to calculate the direction of the field
- μ0 = permeability of free space
μ0 = 4π × 10-7 T m / A
To get the net magnetic field due to the current-carrying segment of conductor:
How can we apply this to solve a problem?
Applying Bio-Savart
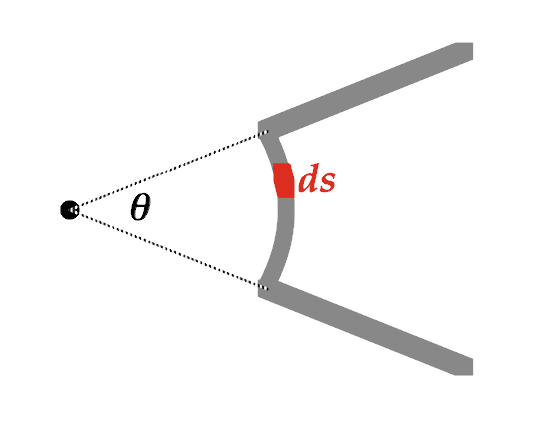
Determine the magnitude and direction of the magnetic field at the point O in the diagram. (Current I flows from top to bottom, radius of curvature = r.)
For straight segments, ds × "hat-r" = 0.
For curved segment, ds × "hat-r" = "ds", because s and r are perpendicular.
12.1.3. Magnetic field near a long, current-carrying wire
If we have a long wire, we can find the total magnetic field due to the sum of all those current segments.
Magnetic field for an infinitely long wire
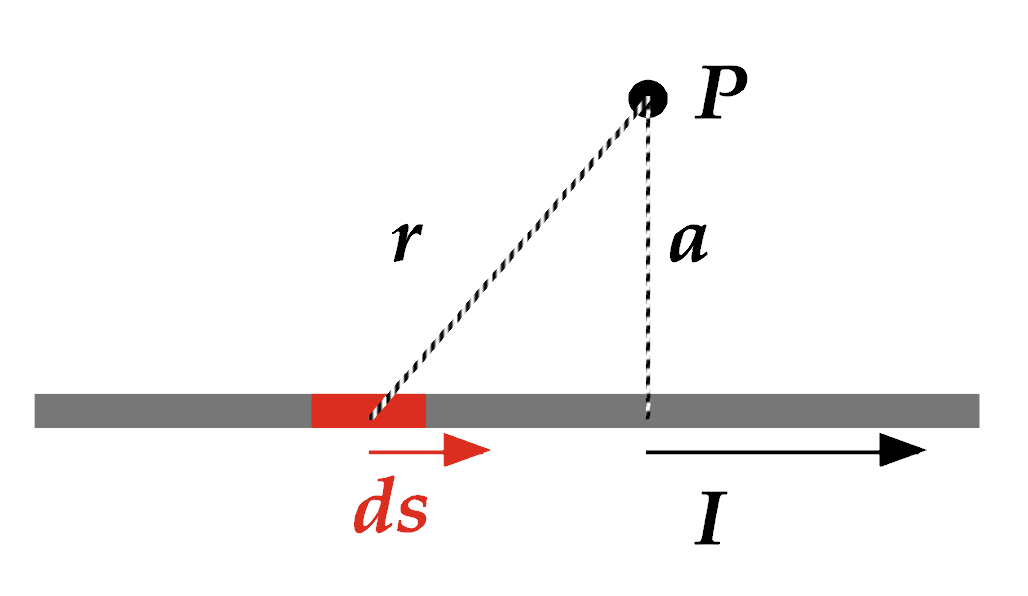
Determine the direction and total magnitude of the magnetic field at the point P shown here, near a long, thin, wire.
Derivation not shown, but... the magnitude of the magnetic field for an infinitely long straight wire is:
Magnetic force between wires

What happens if we have two wires placed parallel to each other, separated by a distance a, each carrying a current? In this example, the wire on the left carries current I1 into the page, and the wire on the right carries current I2 out of the page.
The wire on the left is producing a magnetic field that circles that wire in a clockwise direction. The magnitude of that magnetic field is:
The wire on the right has a current flowing through it, and is thus a current-carrying wire in a magnetic field, and it experiences a force:
It is common to express the force as a "force per unit length" for a calculation like this.
Follow-up question: What is the magnitude and direction of the force acting on the left wire due to the presence of the right wire?
Also, what happens if the currents passing through these wires are both going in the same direction, rather than in opposite directions?
12.2. Ampère's Law
Similar to the way Gauss's Law uses a Gaussian surface to surround a net charge and identify electric field, Ampère's Law allows us to surround a moving charge (current) and identify a magnetic field.
Definition: Ampère's Law
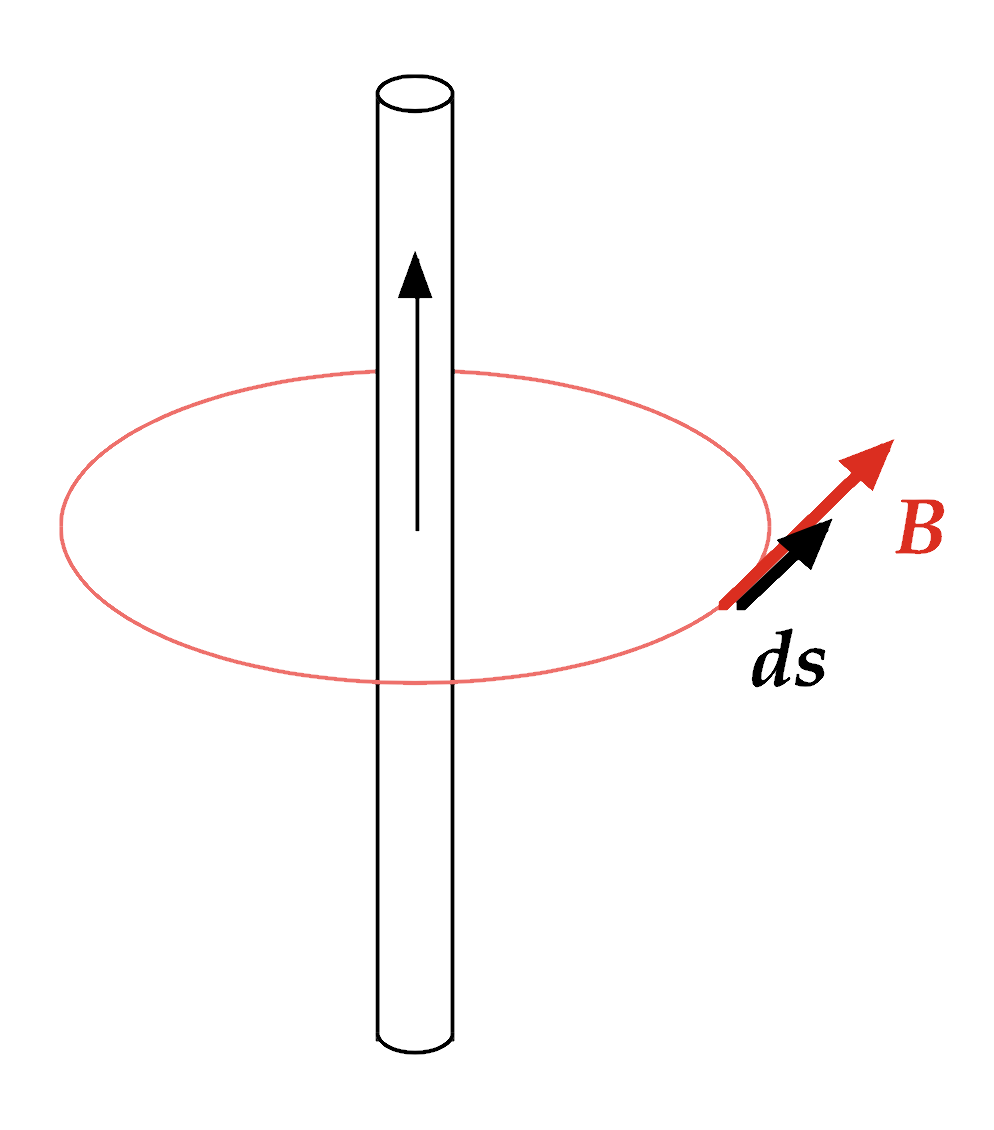
If we evaluate the dot-product B • ds in a circle around a current, and sum this product over the entire path of the circle, we get:
The result is valid for any closed path that encloses a wire conducting a steady current, and is known as Ampère's Law:
Magnetic field around a current carrying wire
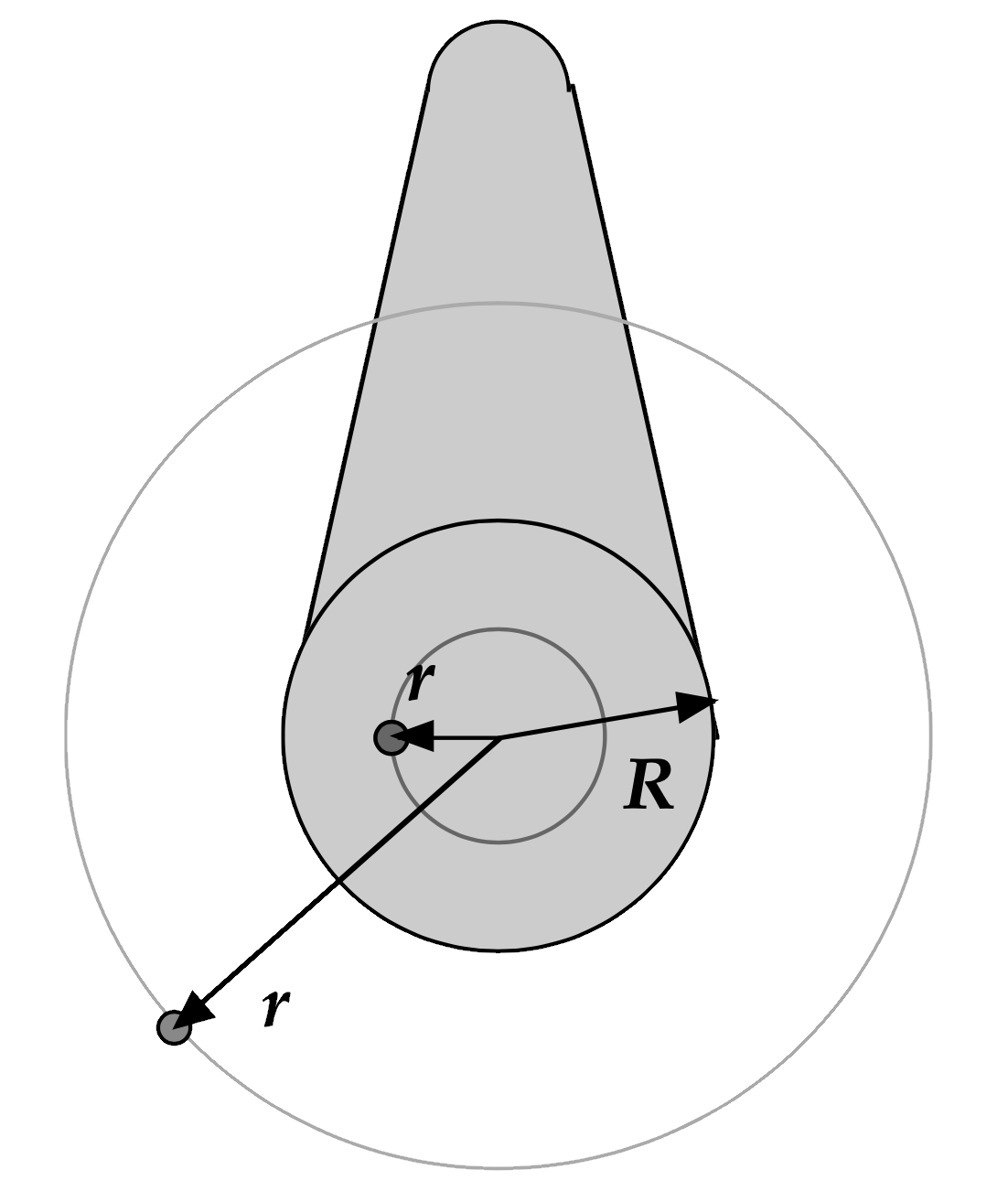
Use Ampère's Law to calculate the magnetic field at a distance r away from the center of a wire of radius R carrying a constant-density current I:
- for a point outside the wire's surface, r > R
- for a point inside the wire's surface, r < R
- When r > R... B = μ0I / (2 π r)
- When r < R... B = μ0Ir / (2 π R2)
Magnetic field near a plane current
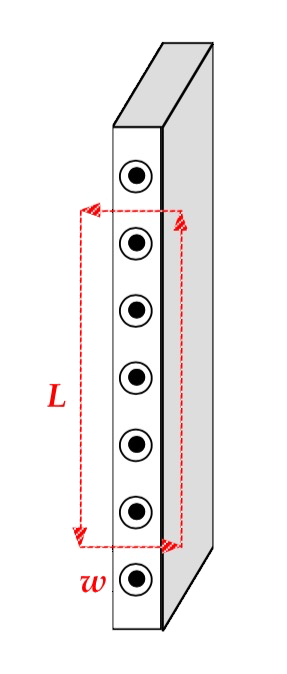
Find the magnetic field B for a thin, infinite sheet of current carrying a current of linear density J in the +z direction.
Draw an Amperian path around a section of the current. The smaller segments of the path pass through the current, where magnetic fields cancel each other out. The longer segments of the path identify the magnetic field on either side of the sheet of current, and can be used with Ampère's Law to calculate the magnitude of the field:
Magnetic field in a toroidal coil

Use Ampère's Law to calculate to calculate the magnetic field inside a toroid of N loops, at a distance r from the center of the torus.
To determine magnetic field inside torus, draw Amperian line inside coil. The wire passes around that Amperian line N times.
In this analysis, we assume that the radius r of the torus is large compared to cross-sectional radius, so B is approximately uniform within torus coils. Also, for an ideal torus (with closely spaced turns of wire), the external magnetic field is close to 0.
12.2.1. Solenoids

An extremely useful component in a variety of electrical and electronic circuits is the solenoid, a long, cylindrical, arrangement of wire wrapped in tight, helical, coils.
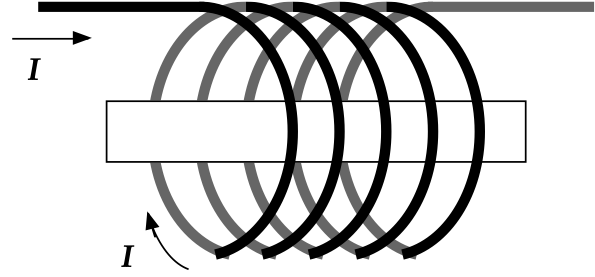
If the turns are closely space and the solenoid is finite in length, the field lines from a solenoid look very similar to those of a bar magnet.
Let's see how we can analyze the magnetic field of a solenoid using Ampère's Law.
Magnetic field of a solenoid
Look at this diagram of a solenoid and consider how the magnetic field contributions from each coil of wire interact with each other.
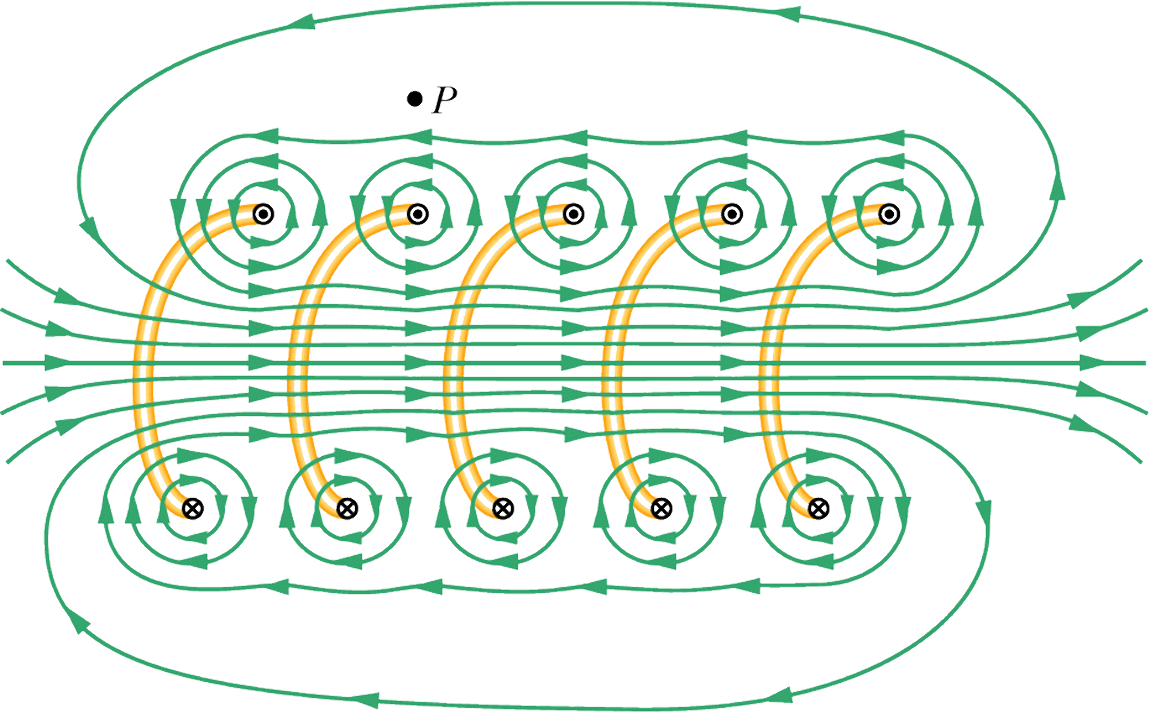
Based on an interpretation of this diagram, we can see that:
- The magnetic field is strongest inside the solenoid, with closely-spaced field lines there.
- The magnetic field is pointing to the right inside the solenoid. We can predict that with a RHR in which our right-hand fingers curve in the direction of current (into the page on the bottom half of the solenoid, out of the page on the top half), and seeing that our right-hand thumb points to the right.
- Outside of the solenoid (at point P for example), there is a very weak magnetic field.
- Between the coils, there is no magnetic field—B contributions from adjacent coils cancel each other out.
To calculate the magnitude of the magnetic field B inside the solenoid, we can draw an Amperian path that encircles some of the current in this circuit:

Notice that not all of the segments have a magnetic field associated with them, so those ds contributions are not considered part of the path total. Segment 1 in the diagram above has a magnetic field there, so we'll include that length in out Amperian path. Segments 2, 3, and 4 don't have significant field, so we don't include them in our sum.
So, if the length of the solenoid is L and there are N loops of wire carrying a current I:
Oftentimes, rather than expressing the magnetic field of a solenoid as a function of coils N and length L, a lower-case n is used to indicate coils-per-unit-length:
12.3. Magnetic Flux
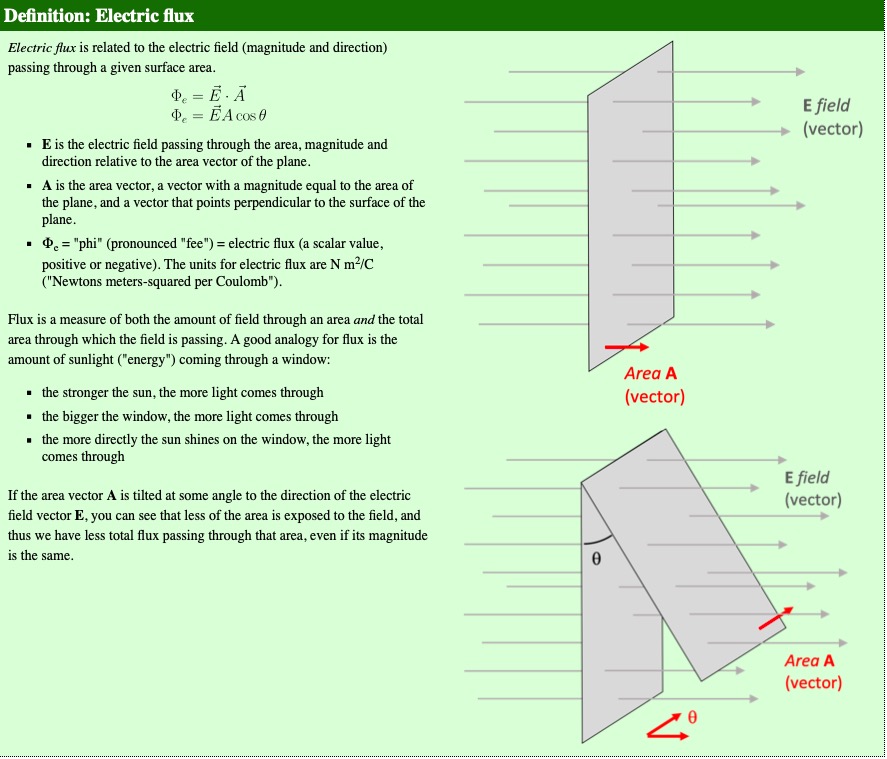
You may recall that electric flux is related to the electric field passing through a given area at a given orientation.
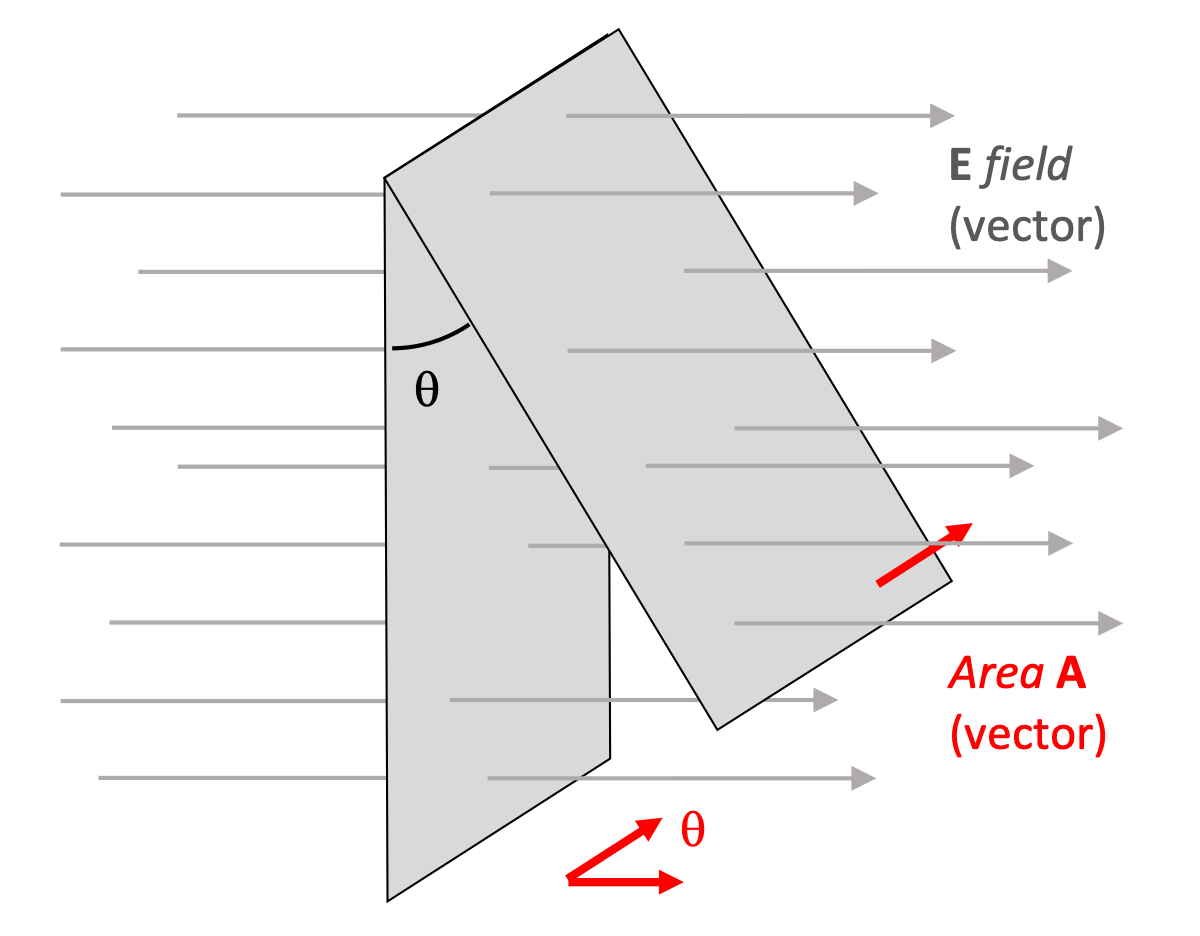
Magnetic flux works exactly the same way.
Magnetic flux near a current-carrying wire
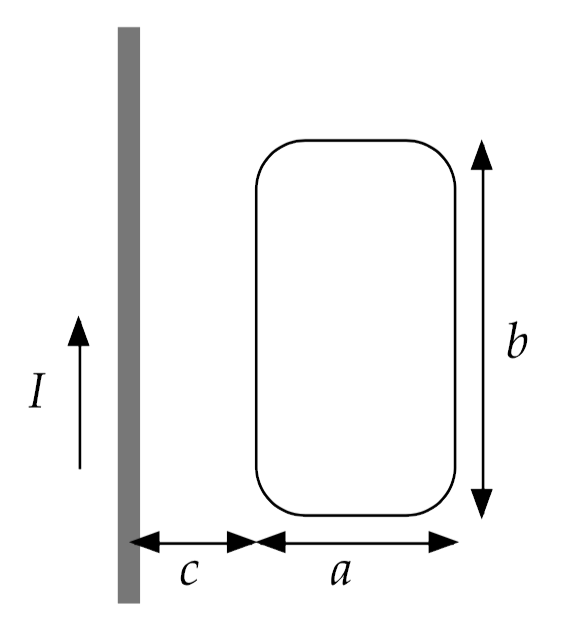
Find the total magnetic flux through the loop shown here.
12.4. Gauss's Laws
You recall that Gauss's Law for electricity is summarized in this equation
... which can be used to identify the electric field in the vicinity of certain charge configurations. One of the key elements of this Gauss's Law is that the net electric flux through a 3-dimensional Gaussian surface depends only upon the internal charge. If there is no net internal charge, there is no net flux through the surface.
Now that we know about magnetic flux, let's look at Gauss's Law for Magnetism.
Definition: Gauss's Law for Magnetism
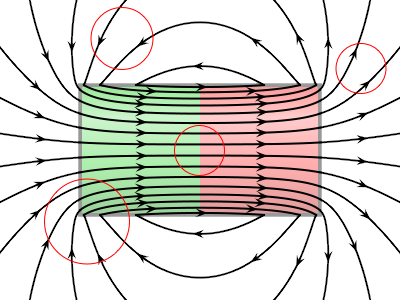
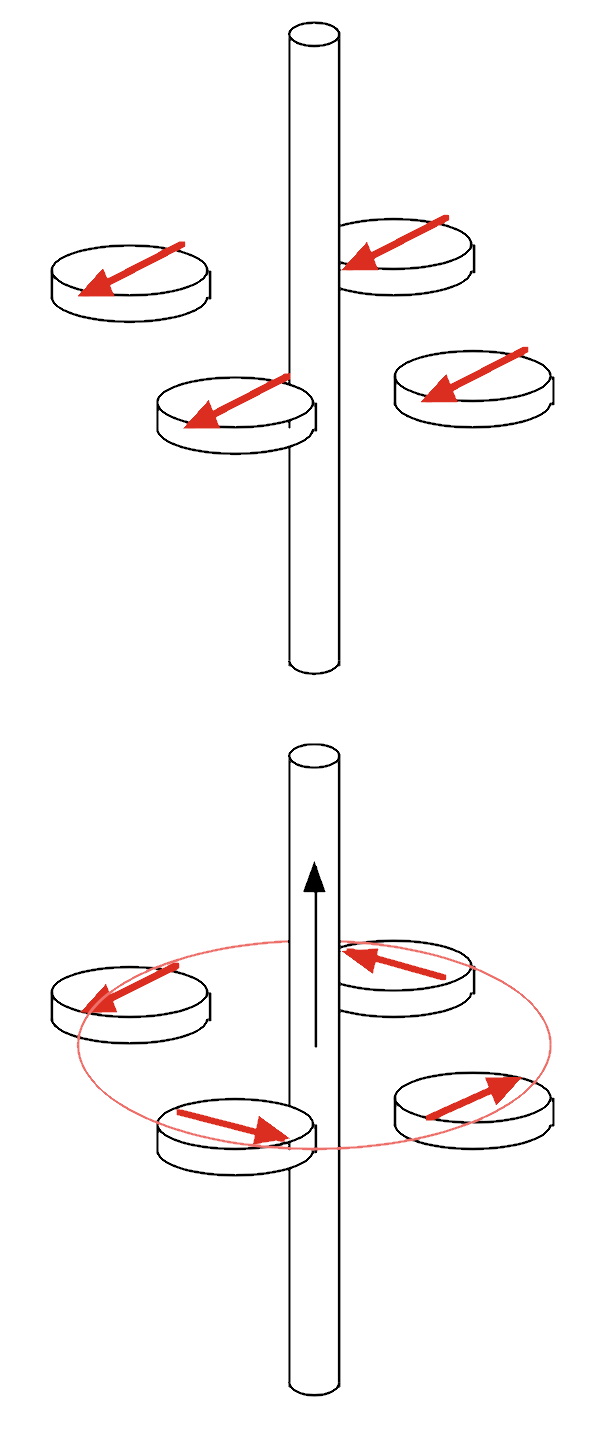
Magnetic field lines are continuous and form closed loops. Magnetic field lines created by currents don't begin or end at any point. Therefore, the net magnetic flux through any closed surface is always zero.
In the figure here, the red-colored Gaussian surfaces show magnetic field lines entering (negative flux) and leaving (positive flux). With an equal number of lines entering and leaving, there is never any net flux.
This is because it is not possible to isolate a single pole of a magnet: there is no such thing as a magnetic monopole. If you cut off the North end of a magnet, you simply get a smaller magnet with its own North and South poles.
12.5. Ampère-Maxwell Law
Coming soon!