Chapter 11: Magnetic Forces and Fields
11.0. Overview
From the topic of electricity, let us now turn our attention to a different, but related, topic: magnetism.
Compasses were in use in China as early as the 13th century BC. The legendary (and possibly mythological) shepherd Magnes had a metal-tipped staff that stuck in magnetic rocks as he walked past. In 1269 AD, Pierre de Maricourt used a simple compass to identify and draw the magnetic field of a natural magnet. He was the one who first described where all the lines meet as a "pole." (Learn more here.)
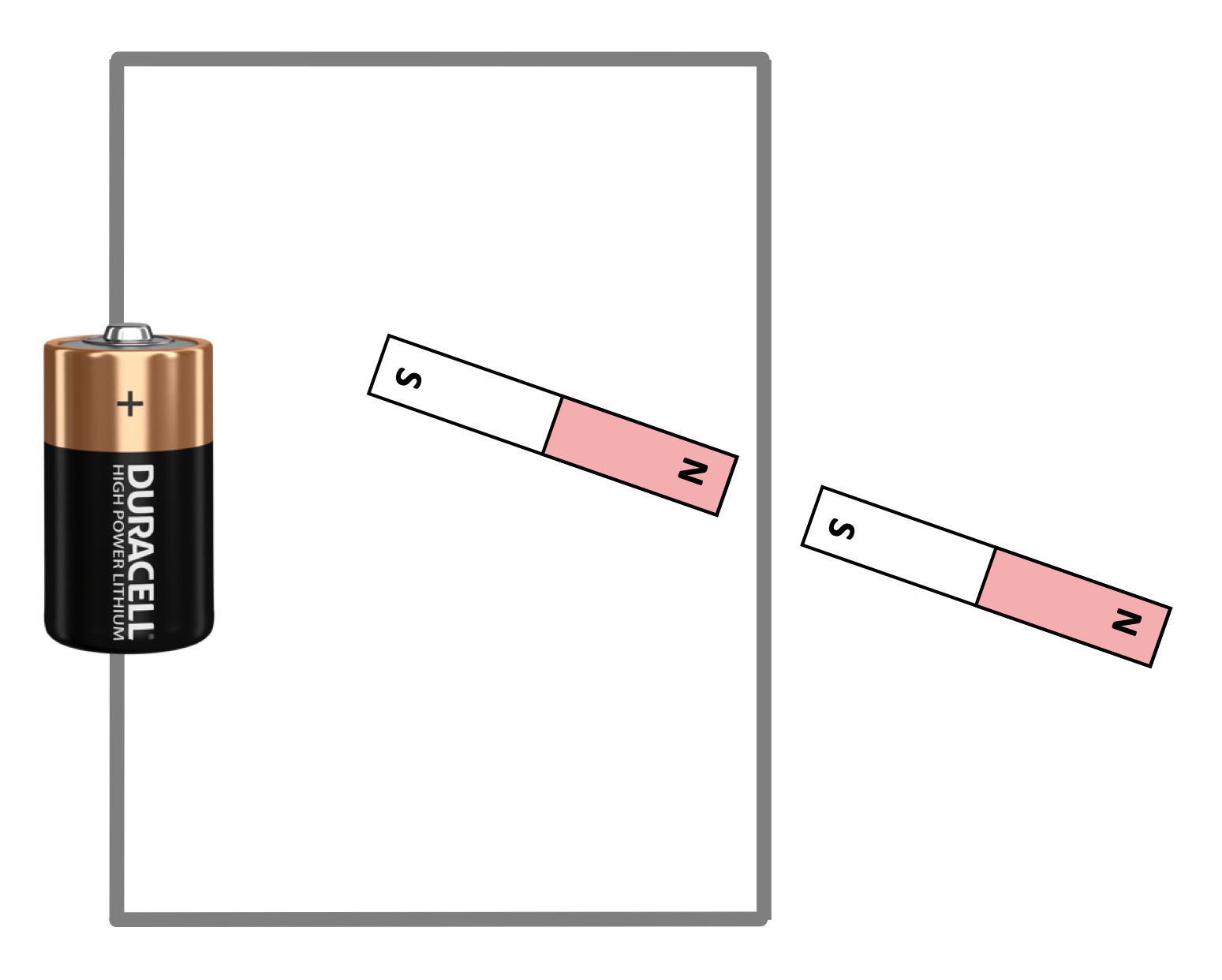
Like positive and negative charges, the North and South poles of magnets interact with each other: opposite poles on magnets attract, and like poles repel. Although there is no direct relationship between electric charges and magnetic poles, there is a strong relationship between electricity and magnetism that we'll be discussing for the rest of our course.
Let's get started!
- Magnets in Magnetic Fields
- Moving charges in magnetic fields
- Currents in magnetic fields
- Torques on coils; the Hall Effect
- The Lorentz Force; Applications
11.1. Magnets in Magnetic Fields

Magnets are made of at least one of the four ferromagnetic elements: iron, cobalt, nickel, or gadolinium.
Magnets have a "north pole," so called because when left to orient itself freely, that end points in the general direction of geographic north, and a corresponding and a south pole.
In a compass, which is simply a magnet free to move around in air or a liquid of some sort, the north pole of the magnet is typically painted red.
11.1.1. The Earth's magnetic field
The direction of a magnetic field is determined by the direction that a compass needle points when subjected to the field. Thus, we can indicate the earth's magnetic field as the idealized diagram shown on the left here, or as the more realistic and complex computer model of the earth's magnetic field on the right.
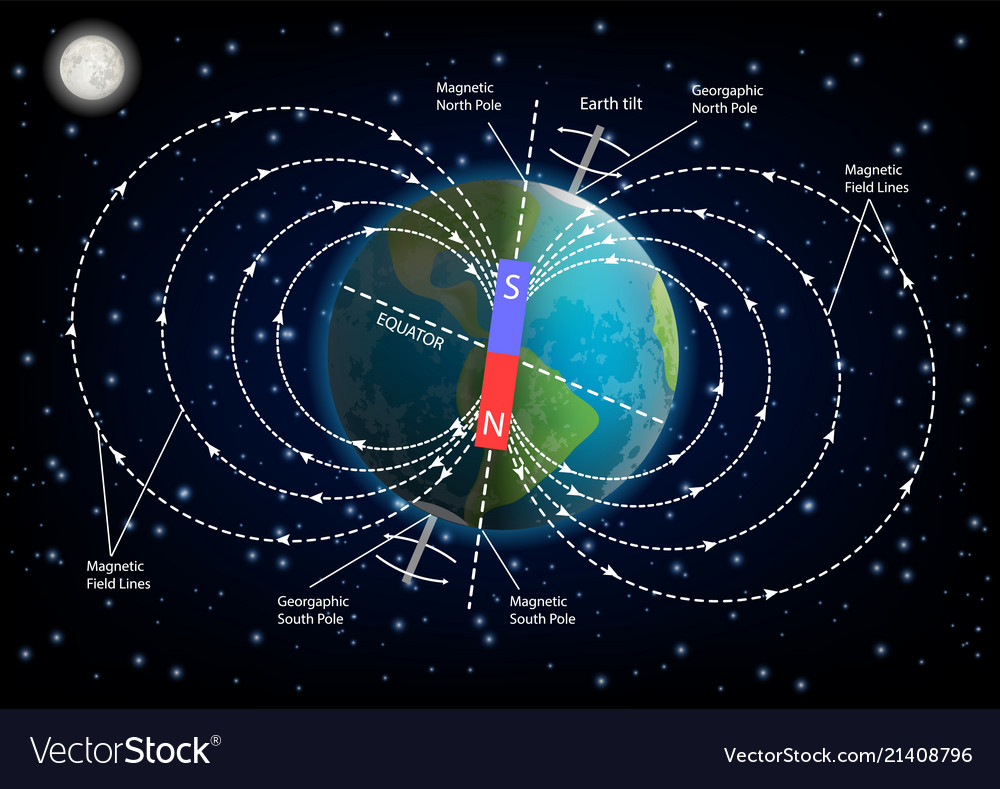
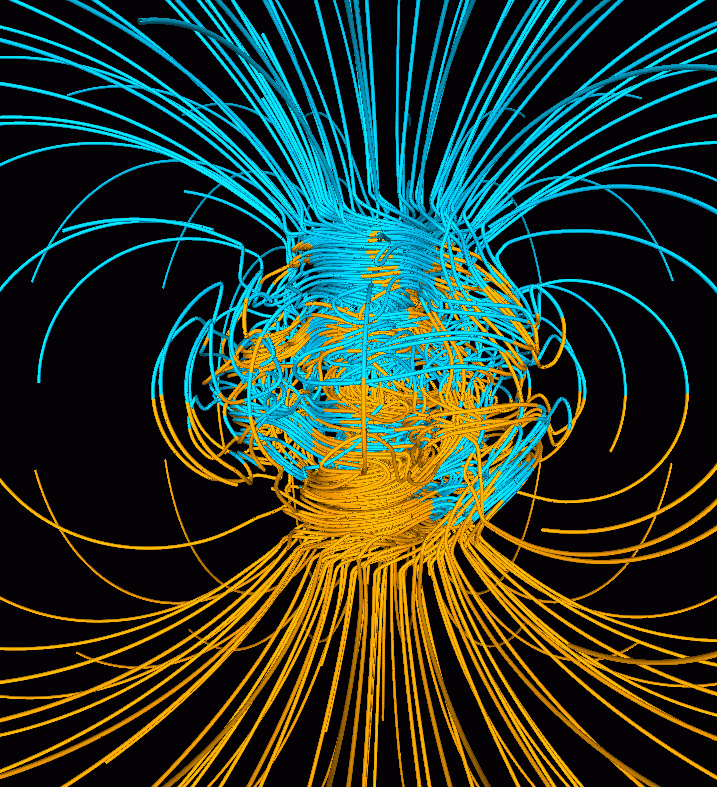
"You're doing it wrong!"
Do a search online for "earth's magnetic field" or something similar. How many diagrams can you find that are incorrect?
It's understandable that this would be confusing. The "magnetic north" is near the geographic north, and so named because they are both at the north end of the planet. But we should (probably) really call it "magnetic south," because if we're going to compare the earth's magnetic field to that of a bar magnet—and they're roughly similar—then that's actually a magnetic south pole up there near our geographic north.
And that's just how it is now. Every ten-thousand years or so the earth's magnetic field flips. When that happens we'll actually have a magnetic north near our geographic north... although our compasses will all have their south poles pointing north then...
I. can't. even.
11.1.2. The magnetic field of magnets
The magnetic field around a magnet depends on a number of factors. We can easily measure the direction of the field simply by placing a compass in the vicinity of the magnet.
Regarding the magnetic field lines around the magnet:
- The magnetic field line has the direction of the magnetic field as its tangent at that point.
- The number of lines per unit area is proportional to the magnitude of the magnetic field at that point.
- The direction of the magnetic field is defined as the direction the north pole of a compass needle would point when placed at that position.
There are actually three kinds of magnetism: ferromagnetism, paramagnetism, and diamagnetism. In ferromagnetic materials—the magnetism associated with most common magnets—the material in the magnet has a permanent "magnetic moment" (orientation), due to microscopic "domains" in which the local moments have a preferential alignment.
Units of Magnetic field
Magnetic field is indicated by the letter B, and we'll explore its vector nature soon.
The unit of magnetic field is the Tesla, where 1.0 Tesla = 1.0 N/C • m/s.
Another unit of magnetic field is the Gauss, where 1.0000 T = 10,000 Gauss.
Earth’s magnetic field has a strength between 30 and 60 μT.
11.2. Moving charges in Magnetic Fields
If you place a charged particle in an electric field, it experiences an electric force.
If you place a charged particle in a magnetic field, it experiences no magnetic force.
But what happens when a charged particle moves in the magnetic field? It experiences a magnetic force!
Magnetic force on a moving charge
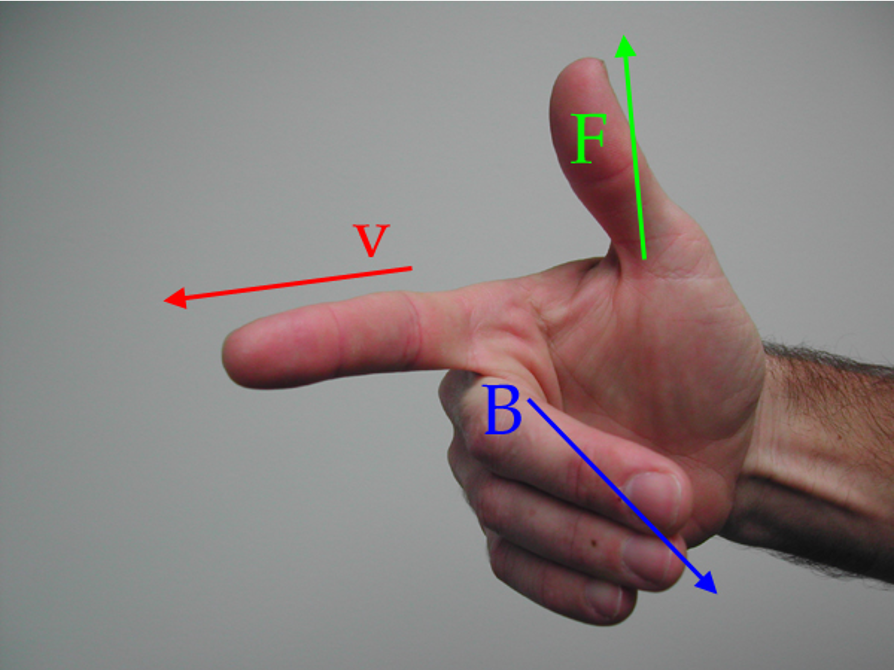
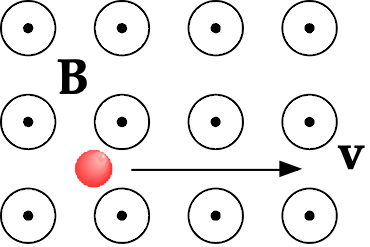
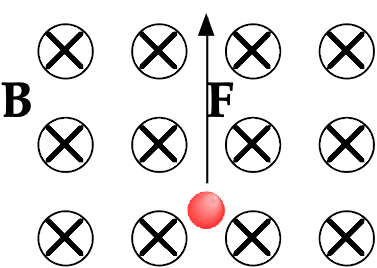
When a particle with charge +q moves at some angle relative to the magnetic field, a magnetic force acts perpendicular to both v and B, as predicted by the Right Hand Rule.
To apply the Right Hand Rule for this analysis, use your right hand and point your index finger in the direction of the velocity for a positive charge. Bend the remaining three fingers of the right hand ("B" for bend, "B" is the magnetic field) in the direction of the magnetic field acting in that region. Your thumb, pointing in a direction perpendicular to the plane formed by the other two vectors, indicates that direction of the magnetic force acting on the positive charge.
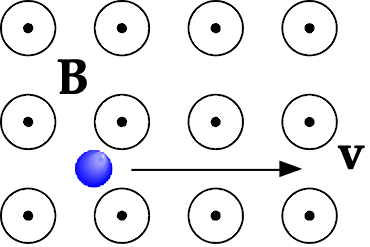
If the charge is negative (an electron, say), you can either reverse the direction of the force that you've just determined, or use an equivalent "Left Hand Rule" for negative charges.
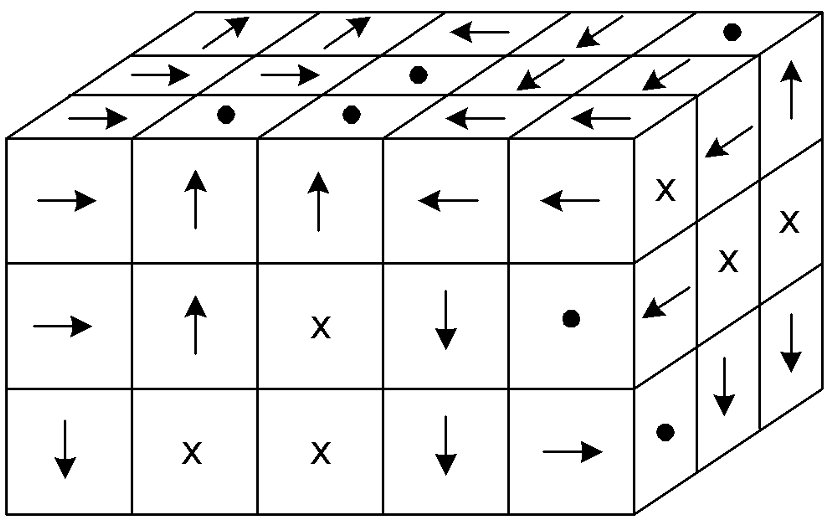
F = qv × B practice
Take a look at each of these diagrams, in which a red positive charge or a blue negative charge is moving through a magnetic field. Identify the direction of the missing vector in each diagram.
Reminder: a vector coming "towards us" or "out of the page" is indicated by a dot, often with a circle around it. A vector going "away from us" or "into the page" is indicated by an X, often with a circle around it.
- Force on the charge is into the page
- Velocity of the charge is out of the page
- Force on the charge is into the page
- Force on the charge is down
- Velocity of the charge is to the right
- Force on the charge is out of the page
- Force on the negative charge is into the page
- Force on the negative charge is up
You may have already noticed some of the finer implications of this effect.
The fine print regarding F = qv × B
- For electric fields, the force due to the electric field FE was parallel to the E field; for magnetic fields, the FB is perpendicular to the B field.
- FB acts only when the charge is in motion.
- FB does no Work on the particle when it's traveling through a constant B field, because FB and v are perpendicular to each other.
Let's try a few more problems.
Particle in a magnetic field
A proton moving upward with a speed of 5.0e6 m/s in a magnetic field feels a force of 8.0e-14 N to the west. When moving horizontally to the north, it feels zero force. Find the magnitude and direction of the magnetic field in this region.
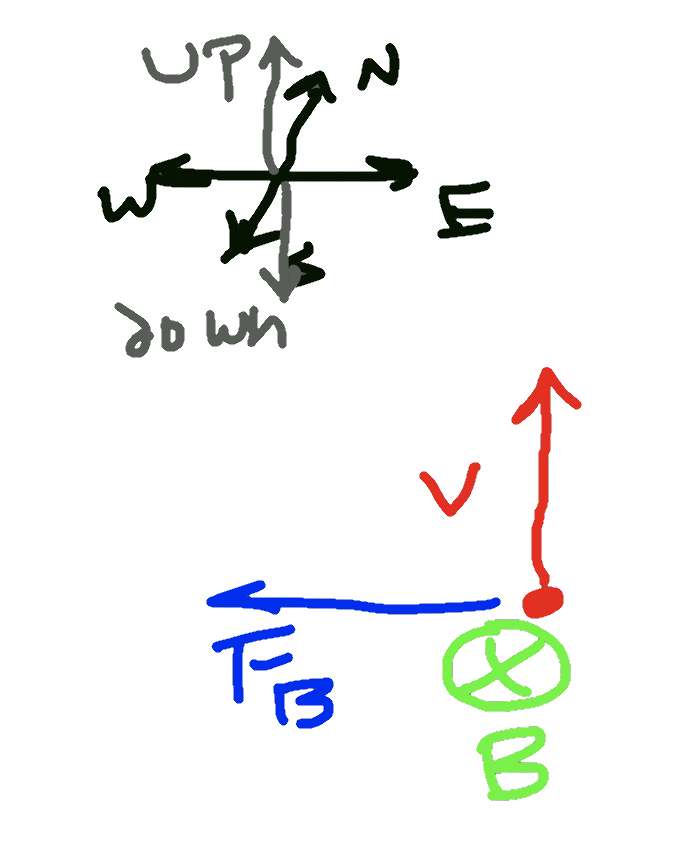
The fact that the particle feels a force when it's moving upward, but not when it's moving north, reveals that the magnetic field must be oriented in the north/south direction, with no components in the east/west direction. We can draw a vector diagram of the forces acting on the particle.
Now that we know the vectors are all oriented perpendicularly to each other, we can calculate the magnetic field B.
Circular motion of charge in a magnetic field
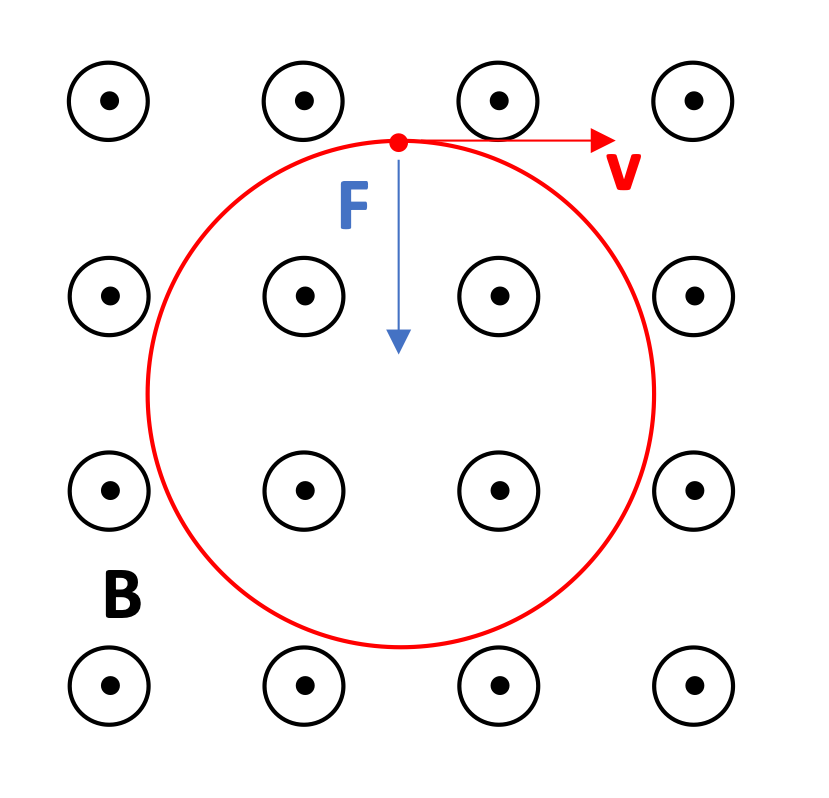
A particle with mass m and positive charge q travels through with a velocity v that is oriented perpendicular to a magnetic field of magnitude B, as shown. Calculate the radius of the circle as a function of the given quantities. Then calculate the angular velocity ω and the period T.
Let's get the radius first, with the magnetic force acting as a centripetal force:
Now, using what we know about circular motion:
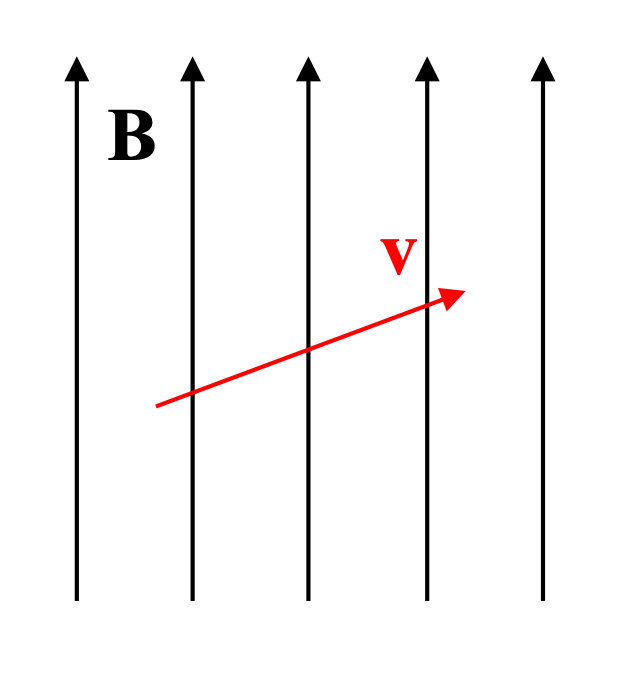
It's relatively easy to determine what happens to a moving particle in a magnetic field when the velocity and the field are perpendicular to each other. What happens when the velocity is at an angle to the field, as shown here?
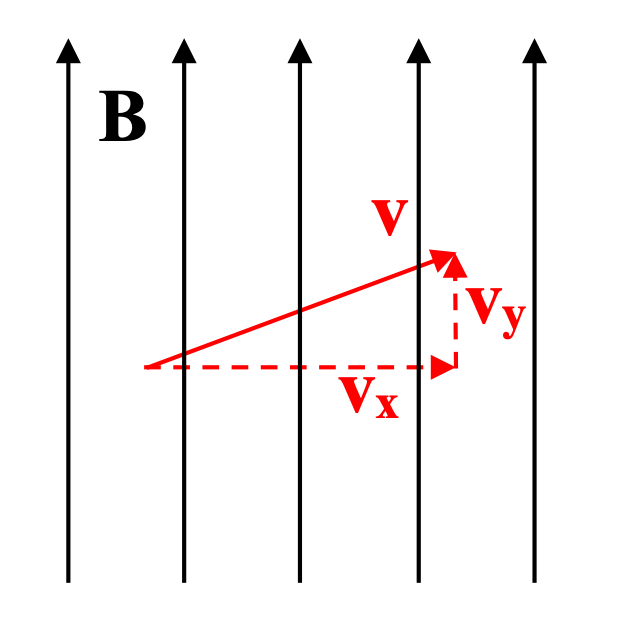
We can consider the velocity of the particle as consisting of two components, one that is affected by the magnetic field, and one that is not. Here, we can see that vy has a v × B that is 0, so that aspect of the particle's motion is unaffected by the magnetic field. In other words, the particle's y-component of velocity is maintained.
The x-component of velocity is perpendicular to the magnetic field. This component is affected by the field, and produces a magnetic force perpendicular to both of those; by the RHR, that force is out of the page. As its x velocity is accelerated in the z direction, its direction of motion changes as the force shifts also. Its circular motion in the x-z plane combines with the motion in the y direction to produce a "helical" path of motion, spiraling upwards.
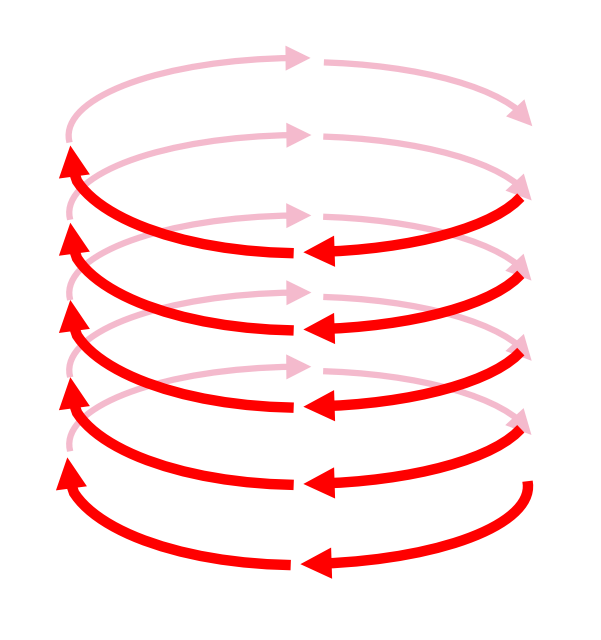
In a constant magnetic field the radius of the helix doesn't change. If the magnetic field gets smaller or larger, the helix assumes more of a "corkscrew" or "pigtail" form.
11.3. Currents in Magnetic Fields
If magnetic fields exert a force on moving charges, then what happens when we have a current-carrying wire exposed to a magnetic field?
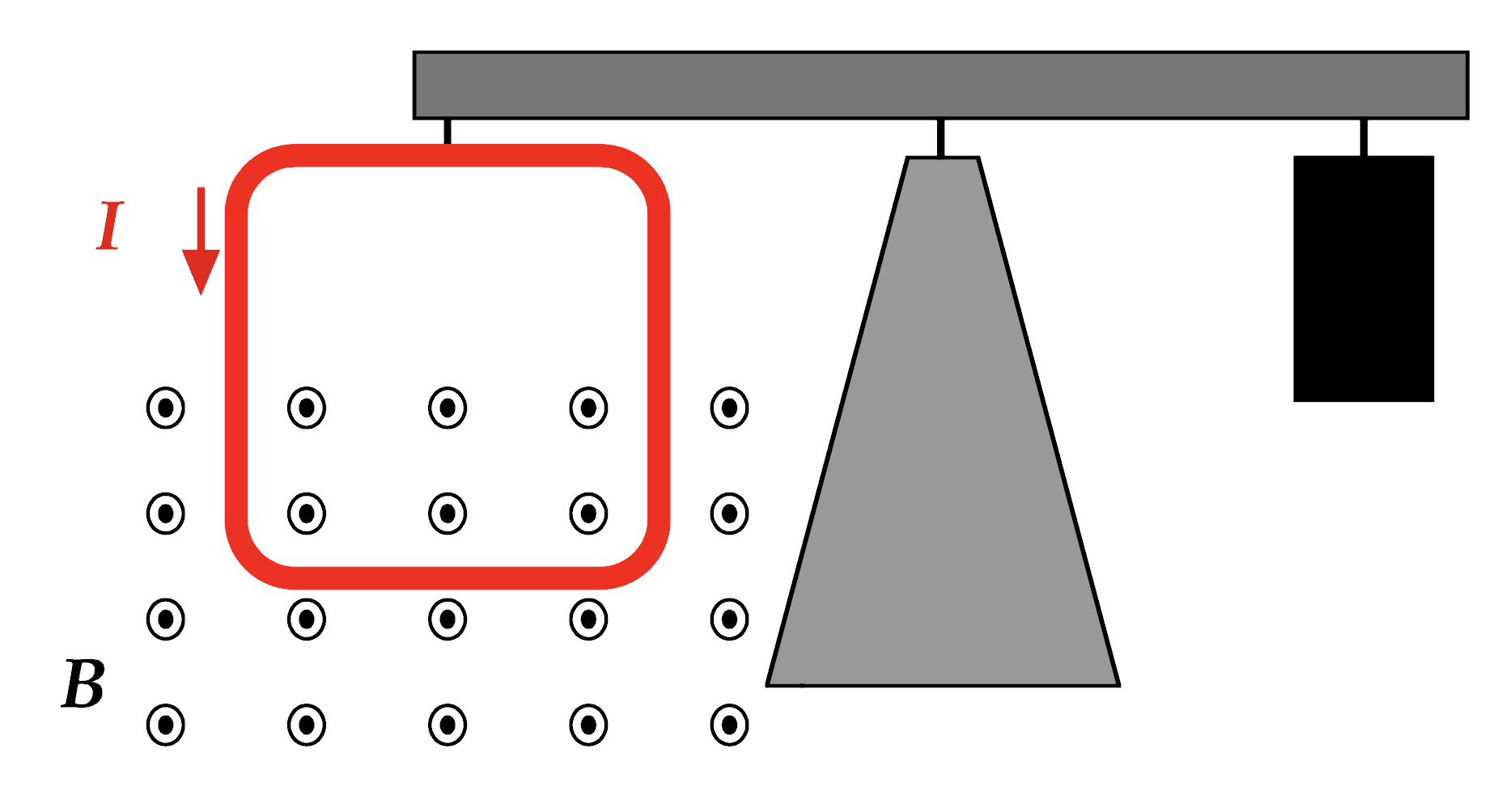
Direction of Force on a wire
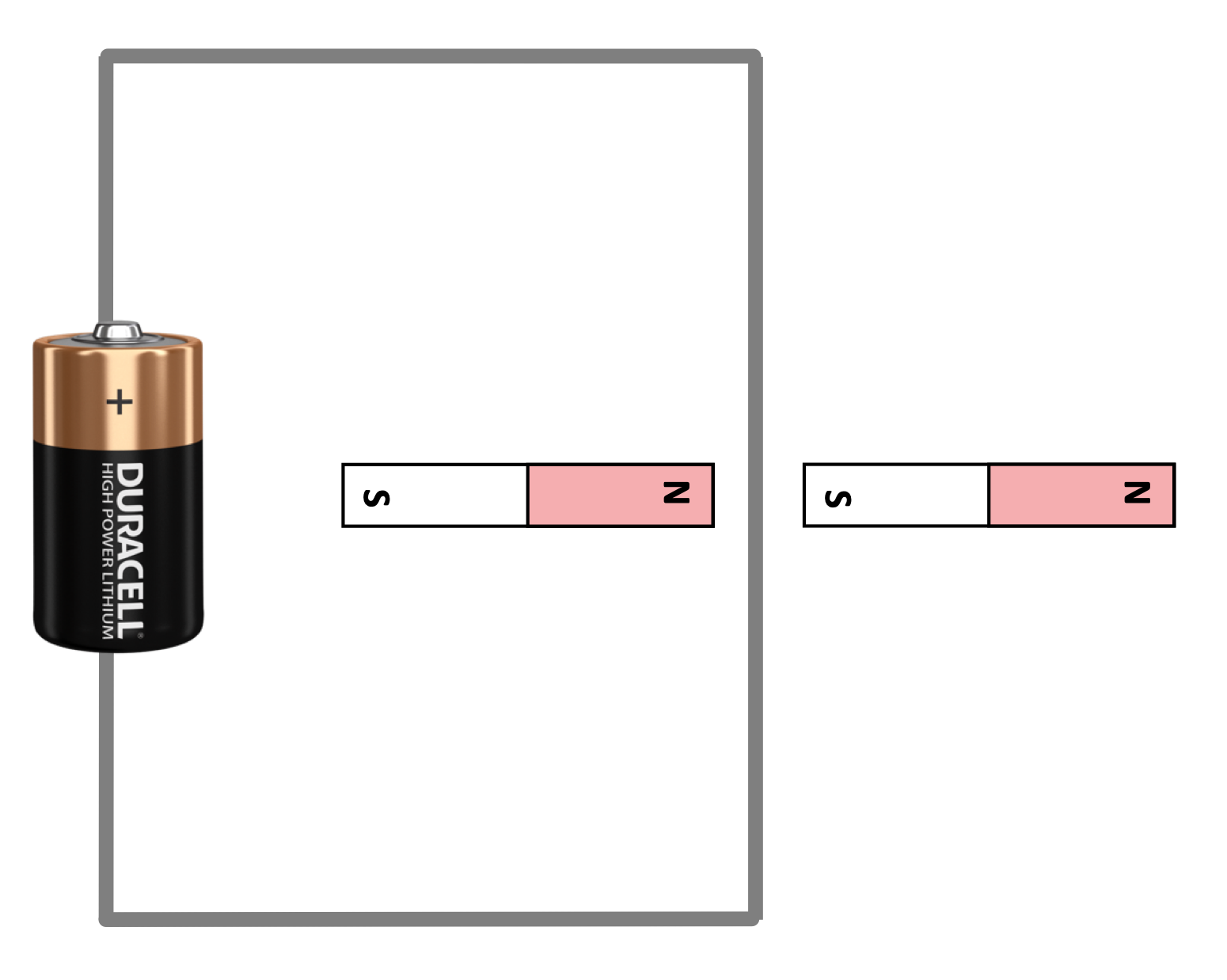
In which direction is the (conventional) current in the wire moving? In which direction is the magnetic field in the vicinity of the wire? In which direction is the magnetic force on the wire?
The conventional current is flowing from high potential (the + end of the battery) through the wire to the low potential, ie. clockwise. The magnetic field points away from North and towards South, or "to the right" in the diagram. Using the RHR with the direction of current and magnetic field, we determine that the magnetic force is "out of the page," or "toward us" in the diagram.
Definition: Force on a current-carrying wire
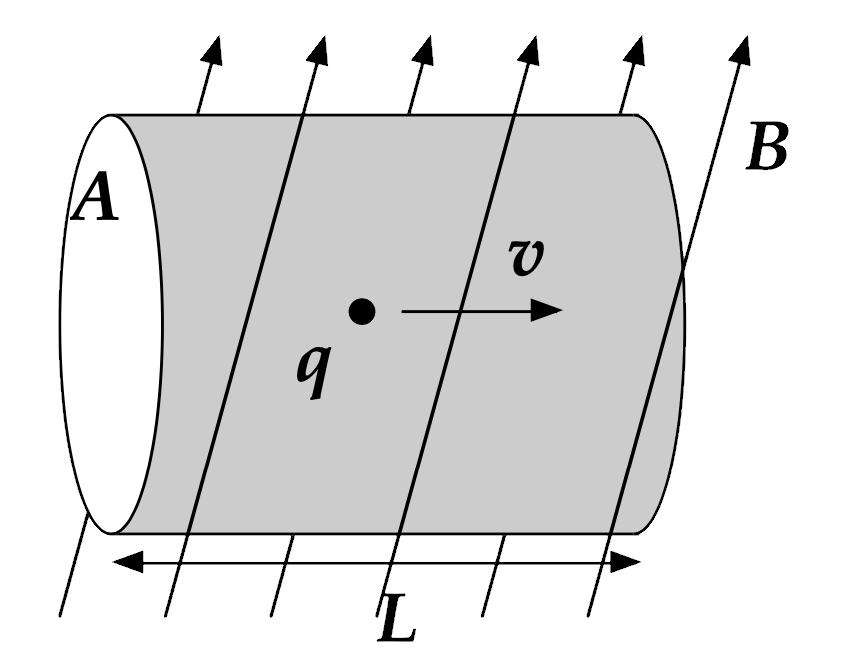
To understand the force acting on the current-carrying wire, we'll apply the "magnetic-force on a moving charge" equation to all the charge carriers:
Now, what is the relationship between those charges moving with a given velocity-drift and current? We'll use that and substitute to get a more useful equations:
Example

A 12 cm length of wire carrying a 30-Amp current runs through the poles of a magnet at an angle of 60° relative to the magnetic field (as shown). If the magnetic field is 0.90 T between the poles of the magnet, what force does the wire feel, and in which direction?
Based on a RHR analysis, the direction of force will be out-of-the-page, or "towards us."
Example
A square loop of wire (10-cm each side) hangs vertically, as shown here. When the current in the wire is 0.245 A counterclockwise, a scale supporting the wire indicates a downward force of 3.48e-2 N. Find the magnitude of the magnetic field.
There are three segments of wire exposed to the magnetic field: two half-lengths oriented vertically, and one horizontal length along the bottom of the square loop. The magnetic forces acting on the vertical loops pull to the left and right, cancelling each other out. Only the bottom segment of wire has a net magnetic force acting on it.
11.4. Torques on coils; the Hall Effect
As we examine the effect of magnetic fields on moving charges, there are two additional interesting aspects to consider.
11.4.1. Torque on a current-carrying loop
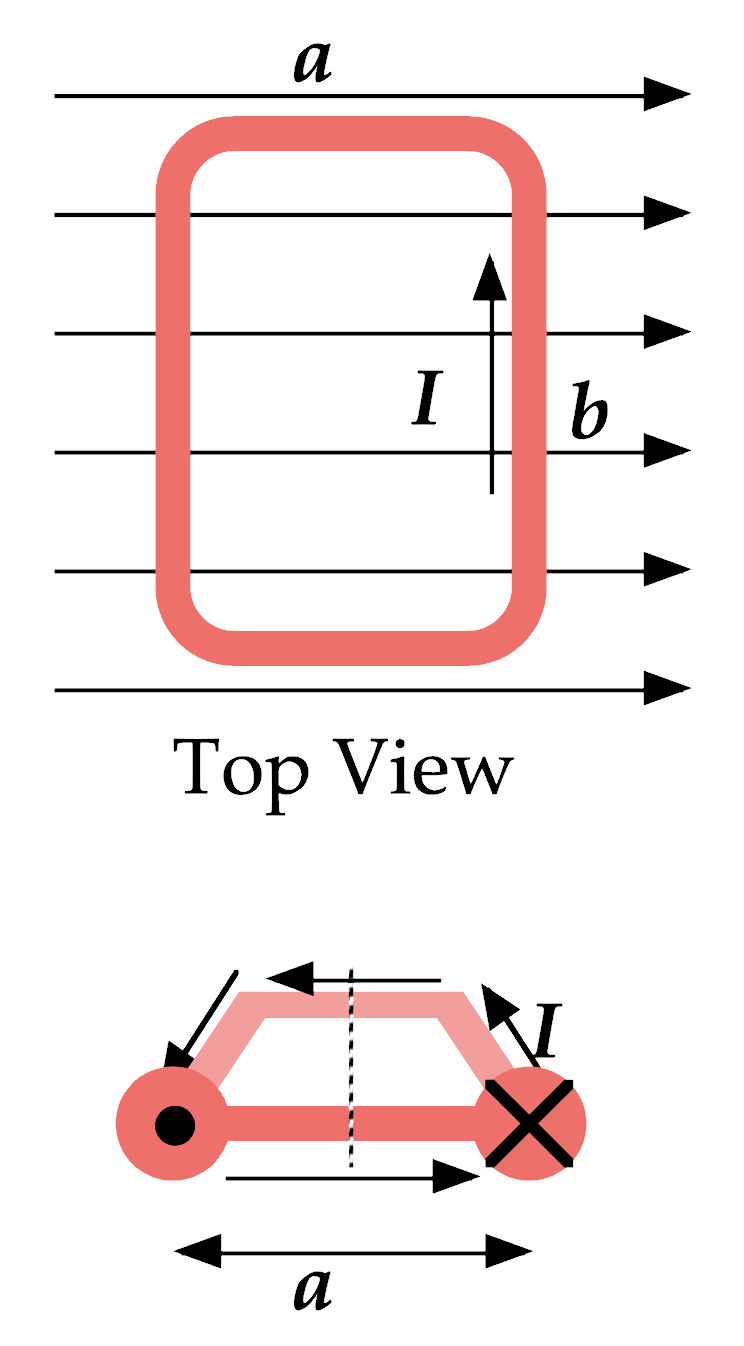
Examine the diagram shown here, which portrays (from a "top view") a current-carrying loop with the plane of the coil aligned parallel to a magnetic field. A tilted "perspective view" of that current loop is shown just below, with the directions of the current indicated as vectors.
What direction is the magnetic force on each of the 4 straight-line segments of the loop?
For the segments parallel to the magnetic field, current I and magnetic field B are parallel to each other. By the Right-Hand Rule, F=ILB sin θ is 0, so there is no force on those segments.
The other two current segments do experience a magnetic force. The left-segment experiences an out-of-the-page force (or "up" for the perspective view) and the right-segment experiences an into-the-page force, ("down" in the perspective view). The net force on the coil is 0, then... but there IS a net torque on the loop.
If we consider the dotted line in the perspective diagram to be an axis of rotation, the current-loop is going to experience a clockwise torque (negative) about that axis.
And this is exactly how an electric motor works!
We can calculate the amount of torque by considering the dimensions of the coil: a/2 is the radius of the torque Force, and b is the length of the wire which has a force being applied to it.
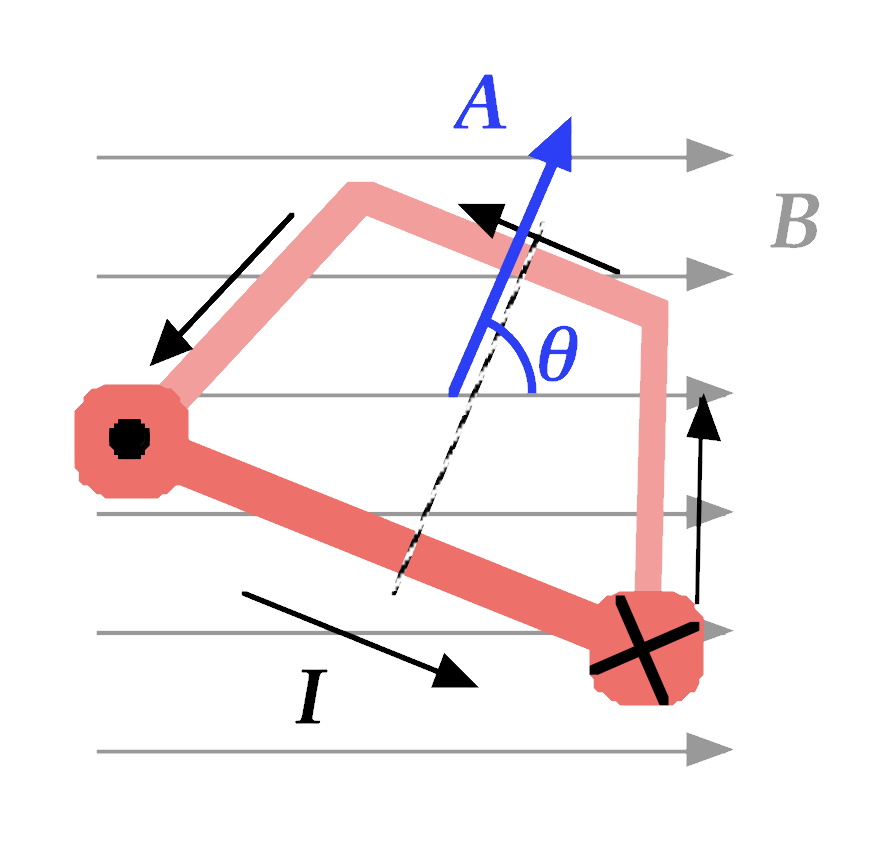
As the loop begins to rotate, the magnetic force acting on the wire remains constant—the length of current remains perpendicular to the magnetic field—but the torque = rF sin θ decreases. We can calculate the torque as a function of θ by considering an area vector for the current loop, with the direction of the area vector determined by using a Right-Hand Rule, with the fingers of the right hand curled in the direction of conventional current in the loop.
11.4.2. Magnetic moment
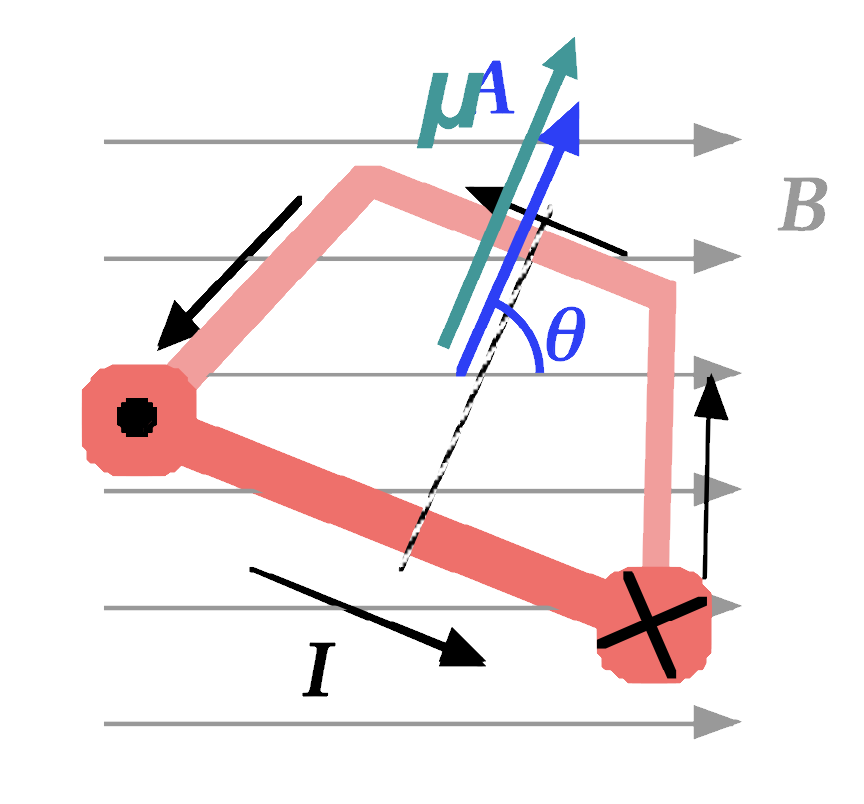
Another way of expressing this torque is by using the magnetic moment μ, where μ is calculated either as IA or NIA:
Example
A rectangular coil of dimensions 5.40 cm × 8.50 cm consists of 25 turns of wire, carrying a current of 15.0 mA.
- Calculate the magnetic moment of the coil.
- If a magnetic field of 0.350 T is applied parallel to the plane of the loop, what is the magnitude of the torque acting on the loop?
- Calculate the magnitude of the torque on the coil then the magnetic field makes angles of 60° and 0° with the magnetic moment μ.
- 1.72e-3 Am2
- 6.02e-4 Nm
- 5.21e-4 Nm, 0
11.4.2. The Hall Effect
We've done most of our analysis of moving charges by focusing on conventional current, which follows the motion of "positive charges". Our various Right-Hand Rules are predicated on consideration of positive charges.
Take a look at the circuit here, in which charges moving across a wide conductor are exposed to a magnetic field.

Which direction would charges move?
If we're tracking the flow of positive charges in the current, those charges will experience a magnetic force while moving in the magnetic field. In addition to the electric force they experience due to the battery in the circuit, which direction will those positive charges experience a magnetic force while in the magnetic field?
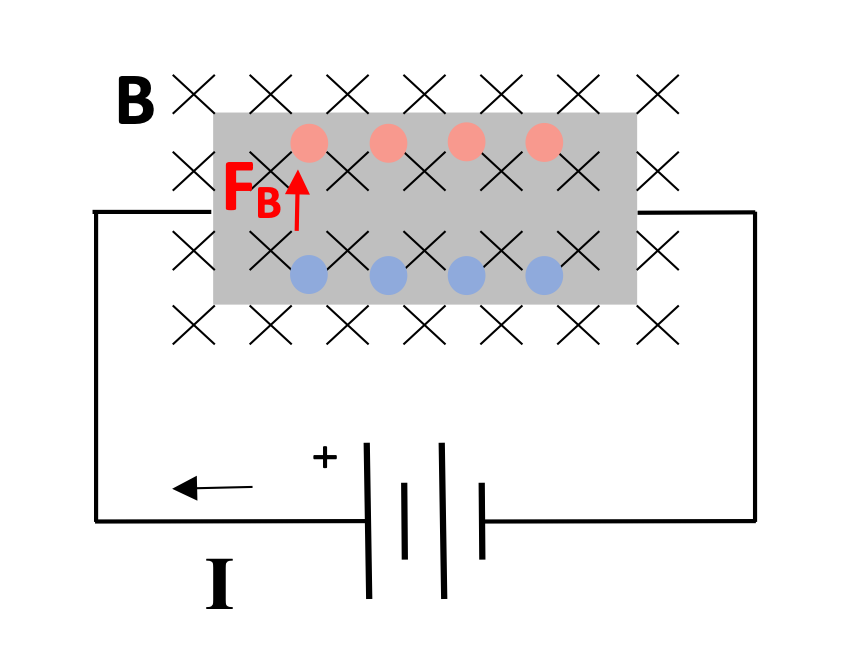
By the RHR, the magnetic field would push moving positive charges up, leaving negative charges on the bottom of the wide conductor.
This would imply a high electric potential along the top edge of the conductor and a low electric potential along the bottom edge of the conductor.
However...
What if instead we were tracking the negatively-charged electrons? What would the RHR predict for that situation?
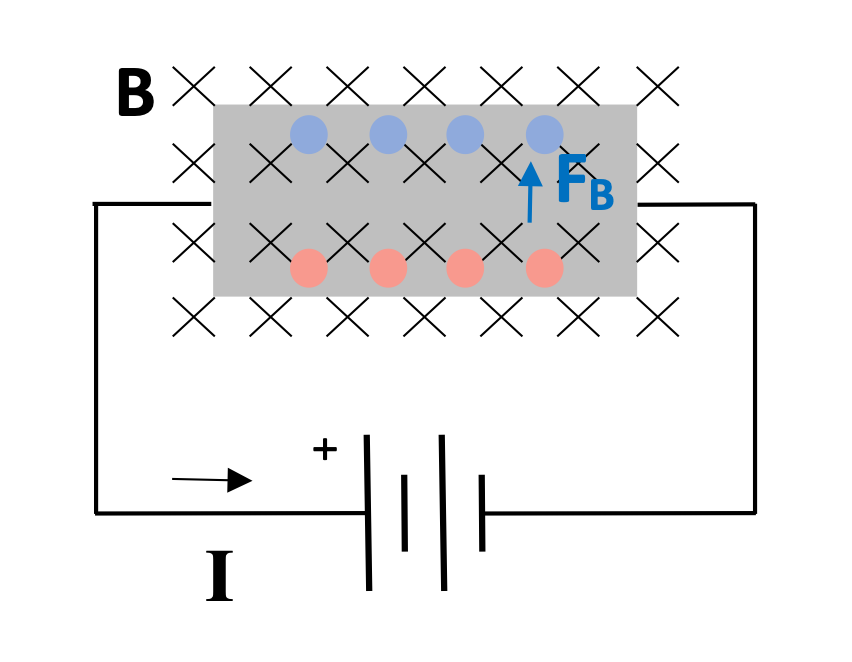
If we track the electrons, our "reversed-RHR" (for negative charges) predicts that it's the electrons that move to the top of the wide conductor, not the protons.
This contradicts the prediction of our earlier analysis. So which is it? They can't both be right!
As you may have guessed, the second prediction is the correct one. The negatively-charged electrons are the particles that are actually moving, and thus the ones that experience a magnetic force.
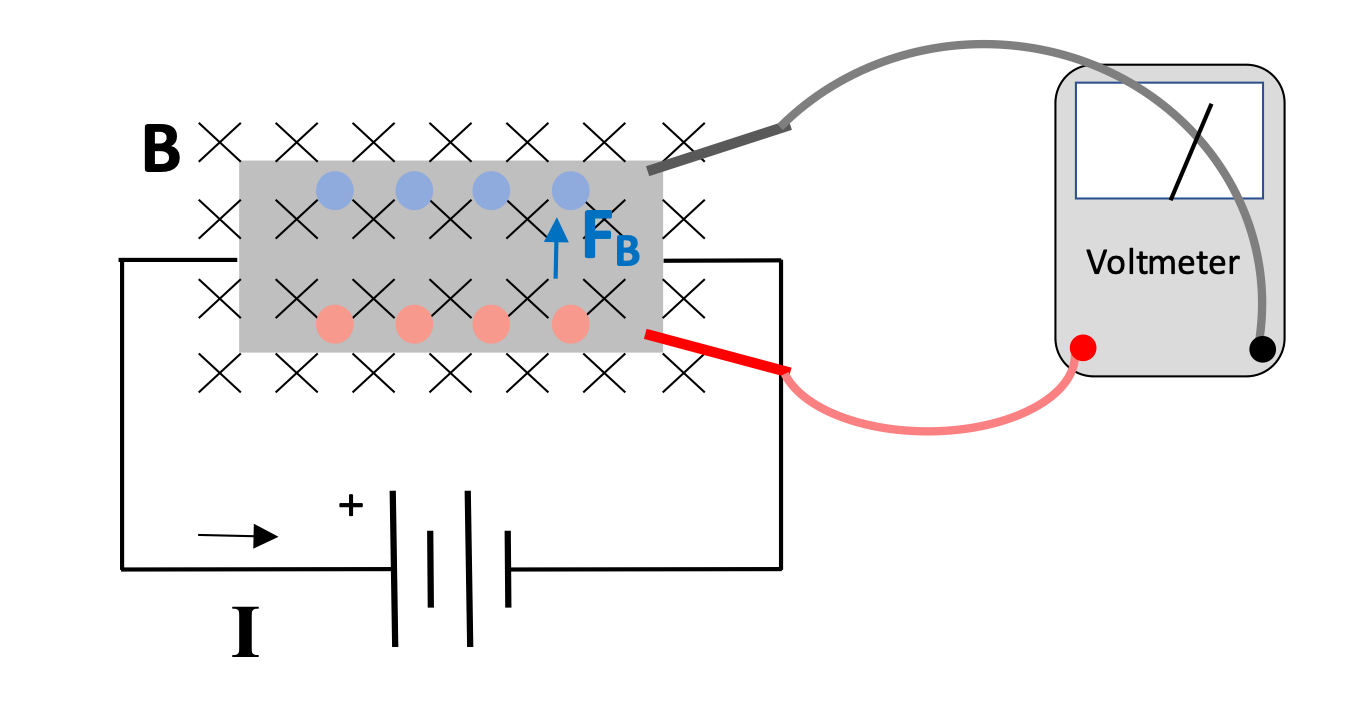
We can confirm that this is the case by performing the experiment and connecting a voltmeter to the upper and lower edges of the wide conductor. The lower edge is the one at high potential, and thus the one where there is net positive charge, while the net negative charge occurs at the upper edge of the wide conductor.
The Hall Effect
The Hall Effect refers to the fact that, when charges form a current moving in one axis through a magnetic field oriented along a second axis, they migrate due to the magnetic force on them, creating a potential difference across a third axis.
The direction of that potential difference can be determined by considering the magnetic force on the actual charge carriers, ie. the electrons.
11.5. The Lorentz Force
We've already learned that an electric field exerts a force on a charge particle, and now we know that a magnetic field can exert a force on a moving charged particle. What happens when we have a charged particle that is moving through a region of space that includes both an electric field and a magnetic field?
Definition: The Lorentz Force
The Lorentz Force is a term used to describe the combination of these two effects, acting on charged particles as they move through electric and magnetic fields.
There are a number of interesting applications of the Lorentz force.
11.5.1. The Velocity Selector
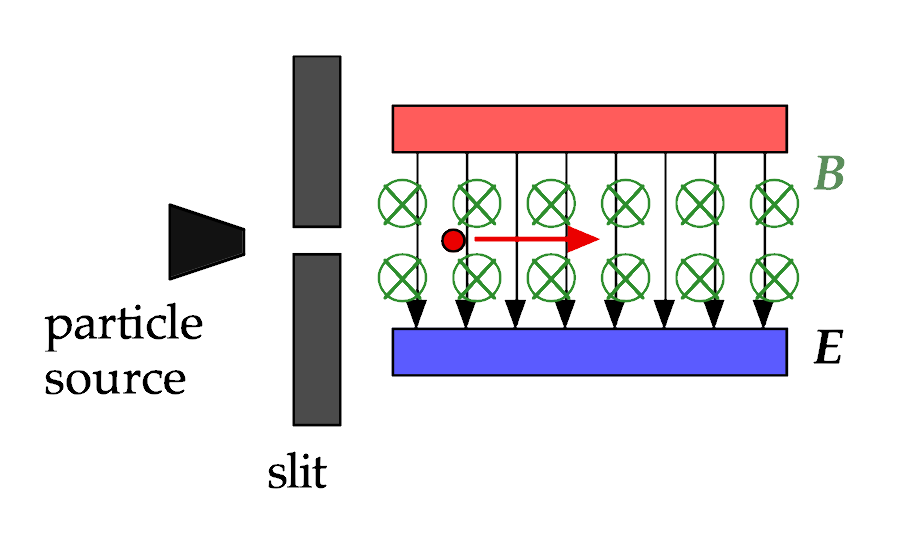
Consider a particle source that ejects positive charges with a velocity v of unknown magnitude to the right, as shown in the diagram here. After passing through a small slit, the positive charge enters a region where there are two charged plates creating an electric field E pointing downwards, and a magnetic field B directed into the page.
In what direction is the electric force (due to the electric field) acting on the charged particle as it moves through this region?
In what direction is the magnetic force (due to the magnetic field) acting on the charge particle as it moves through this region?
A velocity selector
A velocity selector is a device that only allows particles of a chosen ("selected") velocity to emerge. It consists of a particle source with a slit in front of it, electric and magnetic fields (E and B) that can be programmed to have varying magnitudes, and a slit on the far end through which only particles of the chose velocity will pass through.
Given a particle of mass m and charge +q, what electric/magnetic field values will allow only particles with velocity v to emerge from the second slit? (Find v as a function of any of the given quantities.)
Follow-up questions: What happens to charged particles that are traveling with a speed less than v? What happens to a particle traveling with a speed greater than v?
Charged particles traveling with a lesser speed will experience a less magnetic force upwards, even as they still feel the same electric force downwards. Thus, they have a net force down, and the will accelerate downwards, missing the slit and colliding with the wall of the velocity selector.
Charged particles traveling faster will experience a greater magnetic force upwards, and thus experience a net acceleration upwards, missing the slit and colliding with the wall of the velocity selector.
Only particles traveling with a velocity that results in equal electric and magnetic forces will be able to emerge from the selector. By programming E and B field values into the selector, a physicist can be assured of having particles traveling with a specific velocity when they emerge.
11.5.2. The Mass Spectrometer
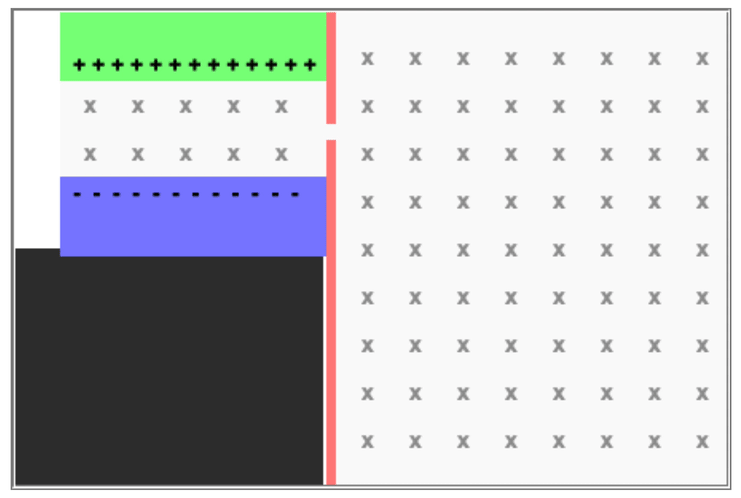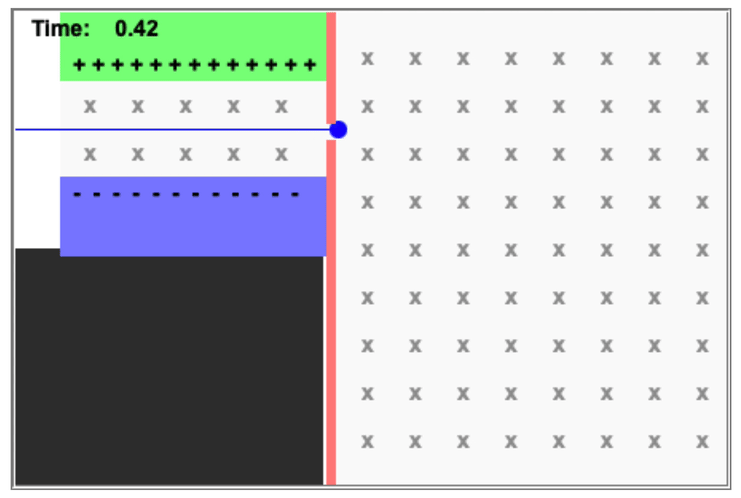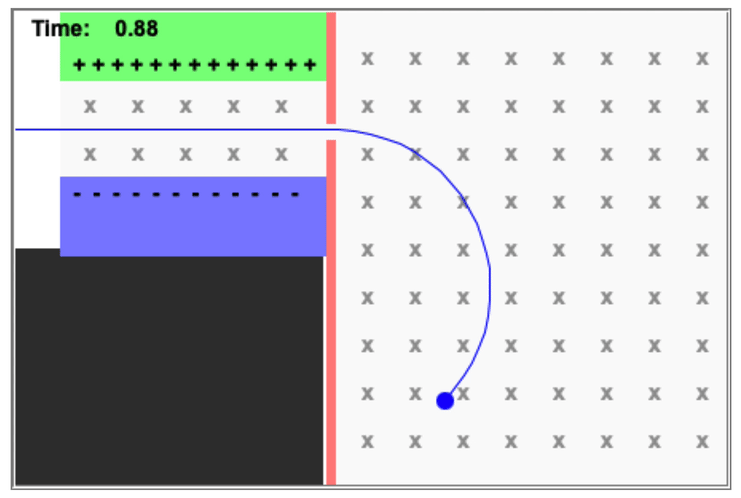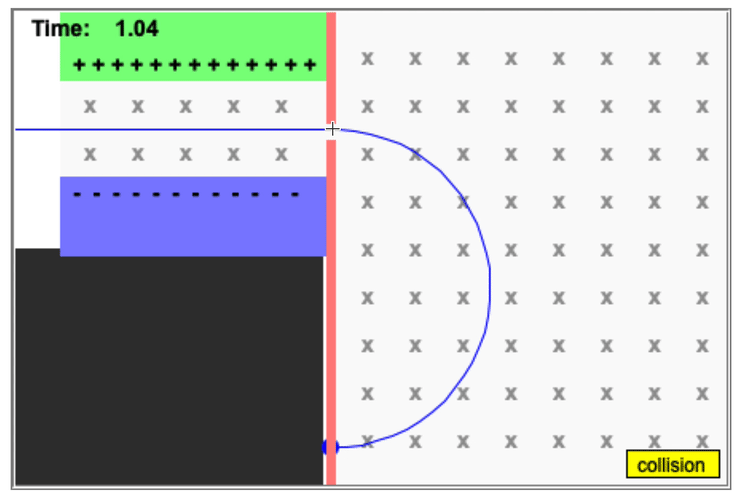
A mass spectrometer ("mass spec") is a device that begins with a velocity selector, and then takes the particles that emerge and places them in a magnetic field only, causing charge particles to move in a circle. All of the particles have the same velocity, but they will travel in circles of different radii according to their mass/charge ratio.
This has a number of interesting applications, including being able to identify different isotopes of the same ion. A particle with more neutrons (higher mass but no additional charge) will have a different radius of curvature. Different ions can be selected for as well.
A mass spectrometer
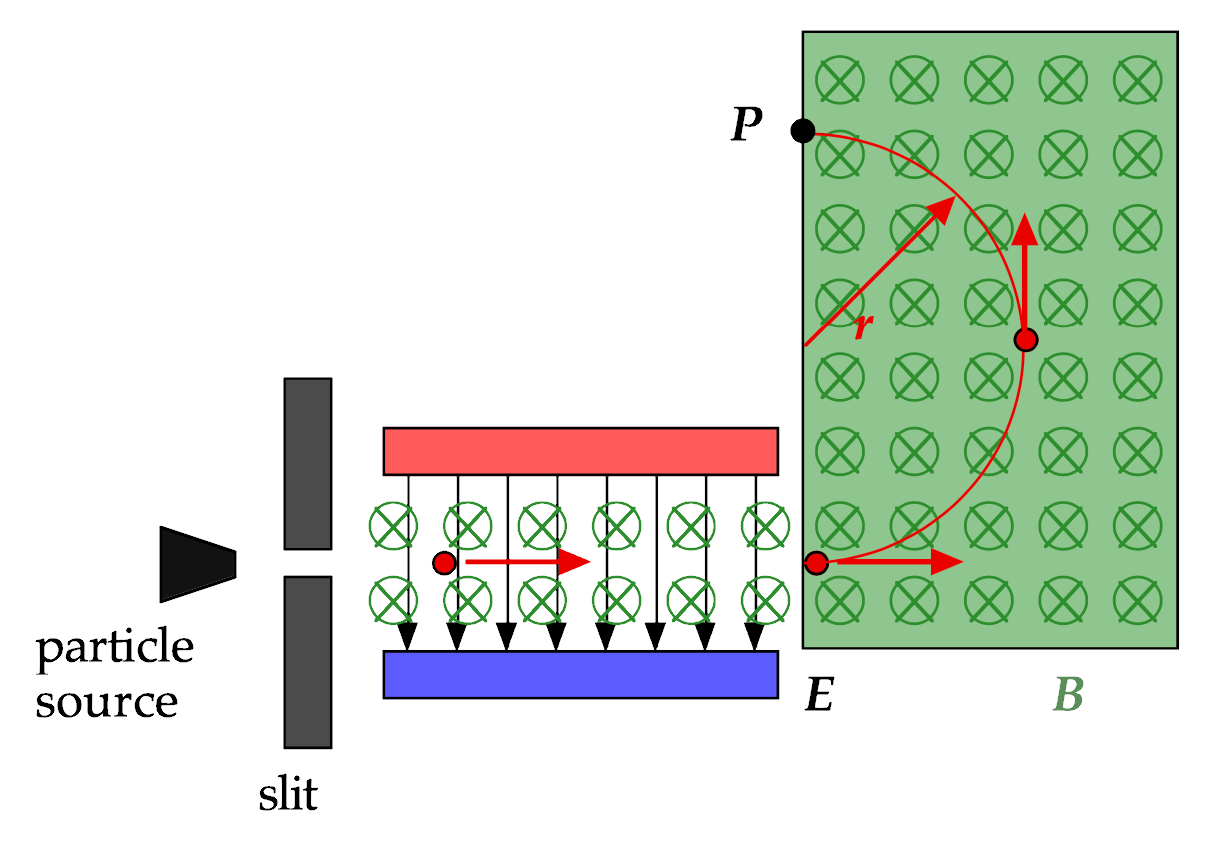
A particle of mass m and charge +q passes through a velocity selector which has an electric field E and a magnetic field B1 as shown. When it leaves the velocity selector it enters a region of magnetic field B2, where it moves in a circle of radius r.
What is the mass/charge ratio for this particle?
Let's first solve for the velocity of the particle coming out from the first set of fields, E and B1 (identified as a separate field in the problem statement but not in the diagram):
And now let's solve for the behavior of the particle in the magnetic field B2 after the particle leaves the selector.
By adjusting B1, B2, and E appropriately, we can measure the radius r of the particle to identify its mass-charge ratio.