
Chapter 9: Conservation of Momentum
9.0. Overview
There are three big conservation laws in the field of Mechanics, and we've just finished studying the first one: Conservation of Energy. The second important law, Conservation of (linear) Momentum, is another important tool that we can use to solve problems, especially when we see two bodies interacting with other via a Force.
Let's get started!
9.1. Linear Momentum
When Newton wrote his Second Law of Motion, he didn't say "A net force causes a mass to accelerate." What he really said (in Latin), was, "Forces applied over a period of time change an object's quantity of motion."
And what does "quantity of motion" mean? There are lots of quantities associated with motion: distance, speed, acceleration, direction of motion... When Newton said "quantify of motion" he was referring to a quantity that we now call linear momentum.
Newton's statement regarding quantity of motion and the Second Law of Motion that we've used in this class are mathematically equivalent.
Definition of momentum
Take a look at this simple derivation that begins with what we've been calling Newton's Second Law of Motion.
The term mv is what Newton referred to as a "quantity of motion," a vector quantity that combines the mass of the object and its velocity.
We use the variable p, a vector, to indicate linear momentum.
So, a net force on a mass causes a change in its momentum p, its mv, where momentum and velocity have been written in bold to remind us that they are vector quantities.
9.2. Impulse
We can talk about this force-momentum-time relationship another way.
Rearranging the relationship above:
Here, the value J represents the impulse applied to the mass, the Force applied through a given amount of time, resulting in a change in the momentum of the object. Note that some authors use I to indicate impulse rather than J.
With this relationship we can talk about the impulse applied to an object, and how its momentum changes as a result.
Determining Impulse
There are effectively four ways that you can identify the impulse acting on an object.
- You can calculate the average force acting over a time period.
- Similarly, if you have a Force-time function you can integrate it with respect to time.
- You can look at a force-time graph and use the area-under-the-curve to determine impulse.
- You can calculate the change in momentum, mΔv, which is caused by the impulse.
Which strategy you use will depend on what you have to work with in the problem.
Cart hitting a wall

A 5.0 kg cart is traveling at 3.7 m/s when it hits a brick wall and comes to a halt. The time of the collision is 0.257 seconds.
- What was the impulse, magnitude and direction, of the wall on the cart in this collision?
- What average force, magnitude and direction, was exerted on the cart during the collision?
- When asked to calculate impulse, one often wants to calculate using Force and time, but impulse can be determined by calculating change in momentum as well. Note that we're indicating directions using positive and negative signs.
- Although the Force is almost certainly changing over time as the wagon collides with the wall, we can easily calculate the average Force of the wall on the wagon. Note that we're indicating directions using positive and negative signs.
Gun firing a bullet
A 10.0 kg gun with an 80.0 cm long barrel fires a 130-gram bullet to the right with a velocity of +400 m/s.
- Calculate the acceleration of the bullet while in the barrel of the gun.
- Calculate the time over which the bullet accelerated.
- Calculate the average Force, magnitude and direction, applied by the gun to the bullet.
- Calculate the impulse on the bullet from the gun, magnitude and direction.
- Calculate the impulse on the gun from the bullet, magnitude and direction.
- Calculate the recoil velocity of the gun.
This type of a problem can be classified as a "recoil" problem: two masses are together at the beginning of the problem, and then a force is applied between them, causing them to move away from each other. We can consider the problem in terms of the masses, the time over which the force is applied, the initial and final velocities of both masses, etc.
As we solve these problems, take a look at the values that we're getting. Do they seem reasonable to you?
- The bullet starts out with an initial velocity of zero, but then after being fired, exits the gun with a velocity of +400 m/s (to the right). Using kinematics to find the acceleration:
- Use kinematics again to find the time of acceleration (while the bullet is moving through the barrel):
- We can calculate the average Force applied by the gun to the bullet using Fnet = ma:
- Based on what we've learned so far we can calculate the impulse using either Force and time, or mass and change in velocity. Either one will work.
These impulses are positive, and thus to the right.
- We could go to the trouble of using the equal-and-opposite force on the gun from the bullet in the opposite direction to do similar calculations, but it should be clear that equal magnitudes of forces over the same period of time will produce equal magnitudes of impulses. The impulse on the gun, however is in the opposite direction, -x in this case.
- We have multiple strategies that we can use here as well, knowing so much about the quantities involved in this problem. Let's use impulse on the gun to find its change in velocity during the firing of the bullet.
9.3. Conservation of Linear Momentum
Two particles that are interacting with each other via some force apply equal and opposite forces to each other (Newton's 3rd Law), for some amount of time t. Because the forces are equal in magnitude and the time of the interaction is the same for both objects, the impulse the objects apply to each other is also equal in magnitude, but opposite in direction.
Take, for example, these two billiard balls that collide in space.
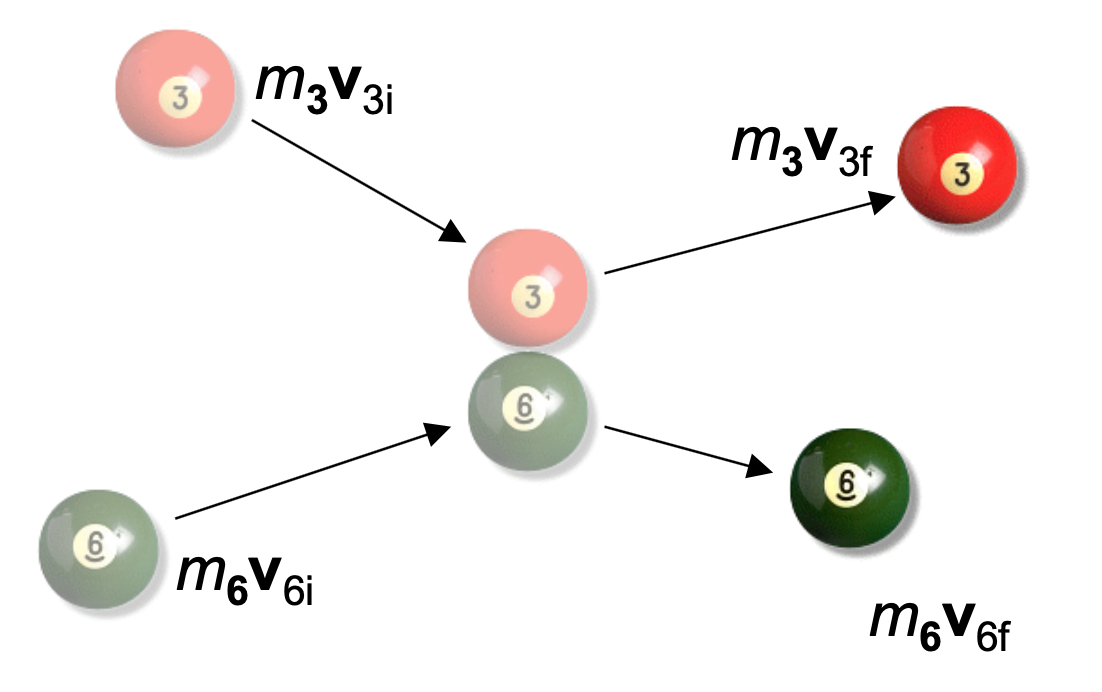
Let's consider the force on the 3 ball from the 6 ball, F3,6, and the force pair, the force on the 6 ball from the 3, F6,3.
In this derivation you can see that we sometimes use "prime" to indicate final values. This is not meant to indicate a derivative.
Law of Conservation of Momentum
"Whenever two or more particles in an isolated system interact, their total linear momentum remains constant."
Ball thrown into a wagon
A 7.5 kg bowling ball is thrown horizontally at 3.2 m/s into a 5.0 kg cart that is initially at rest. The ball lands in the cart and sticks there.
- What is the velocity of the cart after the ball lands in it?
- In one trial the ball doesn't land in the cart, but instead hits the front side of the cart, knocking it forward at 2.2 m/s. What is the velocity of the ball after the collision?
- The problem doesn't describe a direction for the motion, so I'm going to assume the ball was thrown in the +x direction. So:
Because the ball lands in the cart and sticks there, they have the same final velocity, so:
- Now the two masses have different velocities:
9.4. Collisions
We've been discussing how conservation of linear momentum is related to particles that are interacting with each other via a force. One common type of interaction is a collision between two objects, and we can split our analysis up according to the type of collision:
- Elastic collisions
- Inelastic collisions
- Perfectly inelastic collisions
The three types of collisions are similar in some ways, but there are some important differences as well, which will affect how you analyze the situation.
9.4.1. Elastic collisions

Elastic Collision
An elastic collision is one in which there is a negligible amount of energy converted to heat in the process of the collision.
We know that momentum is conserved in collisions, and speaking generally, energy is conserved as well, although in the vast majority of collisions, some energy is converted ("lost") to thermal energy: the bodies colliding become permanently deformed or bent, and the sound of a crash or a crunch can clearly be heard.
But some collisions lose so little energy that kinetic energy is effectively conserved: the total K of all the bodies before the collision is the same as their total K after the collision. In these cases, we say that the collision is elastic.
How to solve an elastic collision problem?
Elastic collisions are so rare that there are just a few circumstances you might consider elastic. Typically collisions between molecules are considered elastic, or perhaps collisions between billiard balls. For some problems you may simply be told to "consider this as an elastic collision."
The equations that you can use to help figure out what's going on are:
9.4.2. Inelastic collisions

Inelastic Collision
An inelastic collision is one in which some energy is converted to heat in the process of the collision.
In this type of collision we have significant amounts of kinetic energy that are are converted to heat in the process of the collision. As a result, kinetic energy is no longer conserved, although momentum still is.
Inelastic collisions are very common. Because the forces involved in collisions are so great compared to the other forces that might be present in a situation—a normal force, a force of gravity, etc.—we typically ignore those other forces and focus on the single force of collision to find out the velocities of the colliding objects just before and just after the collision.
In the photo here, the two cars have collided, and clearly show some damage, some deformation as a result. It takes work to deform a mass, resulting in ΔEinternal. But we can still use conservation of momentum to determine their velocities immediately after collision. (Once the collision is over, friction forces will bring the moving cars to a halt, of course, but for that part of the problem we'd do a different analysis.)
How to solve an inelastic collision problem?
Unless your problem states that a collision can be considered elastic—a very special case—you should assume that your problem is inelastic: some kinetic energy was converted into thermal energy in the course of the collision. We can no longer use conservation of Kinetic Energy in our analysis.
The equation that you can use to help figure out what's going on is:
Demo: Deforming metal and ΔEinternal
Take a length of coat hanger wire and do Work on it by bending a section of it back and forth for 10-15 seconds. Then carefully touch the section that was being deformed. How can you tell that your Work was converted to ΔEinternal in the wire?
9.4.3. Perfectly inelastic collisions

Perfectly inelastic Collision
A perfectly inelastic collision is a special type of inelastic collision, in which the two bodies stick together in the process of the collision. As a result they have the same final velocity after the collision.
Here, too, we see kinetic energy converted to heat, making this a type of inelastic collision. Because the colliding bodies stick together, however, the conservation of momentum analysis is slightly simplified.
One common example of a perfectly inelastic collision is that of a baseball player catching a moving ball in their mitt. Just before the ball is caught, the ball and the mitt have different velocities. After the ball is caught, it and the mitt are together moving with a different velocity: in some cases they might both be moving backwards at a smaller velocity, in other situations they might be moving forward, or even come to a complete halt. It depends on the circumstances.
How to solve perfectly inelastic collision problem?
Perfectly inelastic collisions occur anytime the two colliding objects stick together.
The equation that you can use to help figure out what's going on is:
9.4.4. Example Problems
Ballistic pendulum
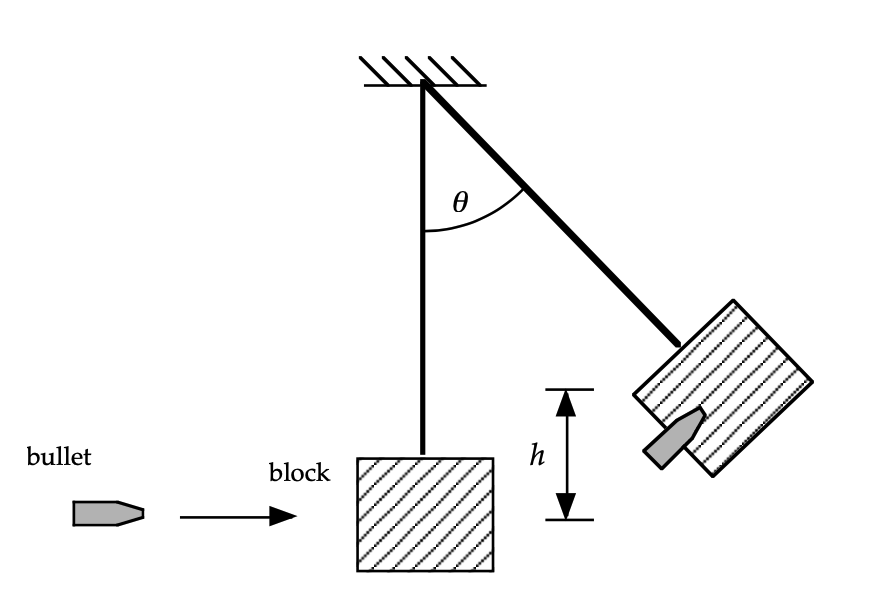
A ballistic pendulum is used to measure the speed of a projectile: a 5.0 gram bullet is fired into a 1.0 kg block of wood. The bullet sticks into the wood, and the bullet-block swing up to a height of 5.0 cm.
- Find the initial speed of the projectile just before it hit the block.
- Find the energy lost in the collision between the block and the projectile.
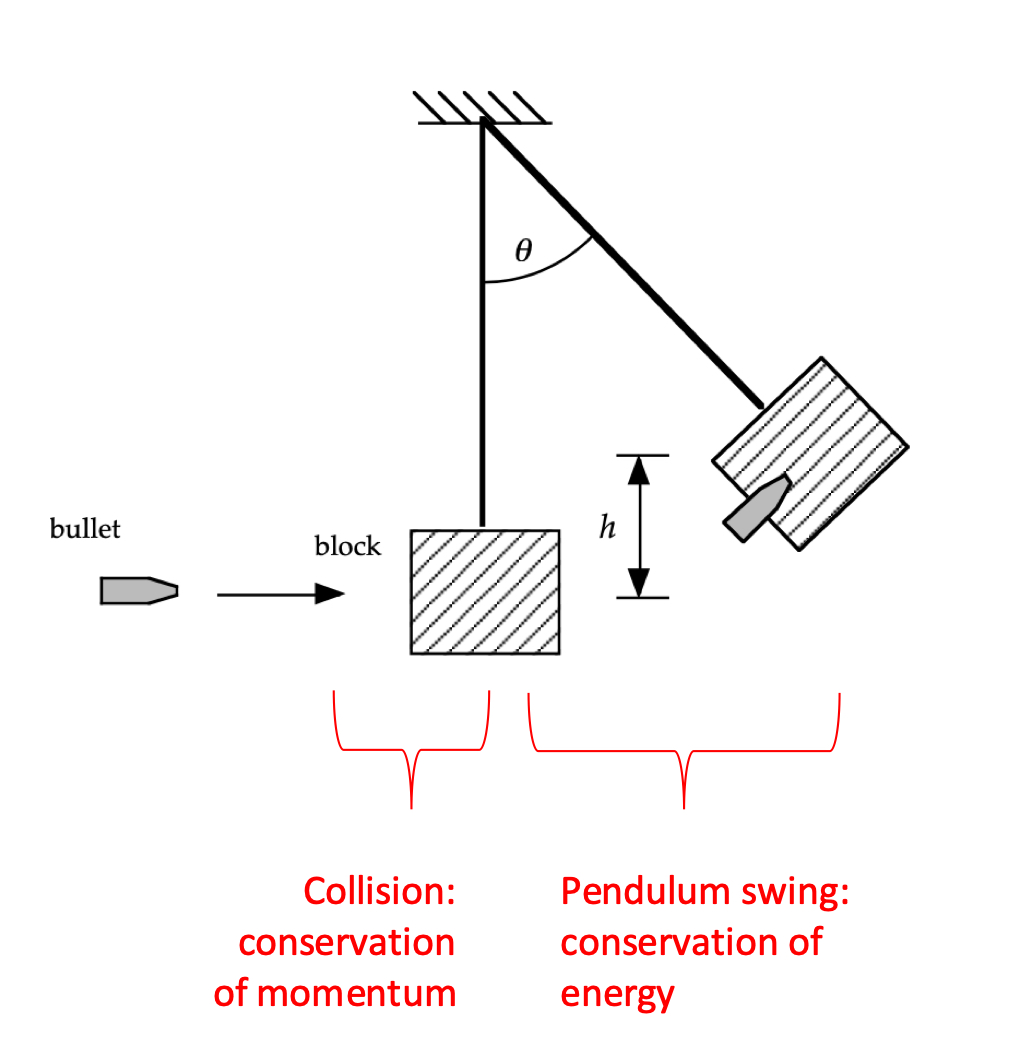
This is a classic problem because it consists of two parts, and because it focuses in on making sure we clarify our understanding of both parts of the problem.
In the first part of the problem the bullet collides with the block, an analysis that we can consider using conservation of energy. Immediately after that collision the bullet-block swing up as a pendulum, which is a conservation of energy problem.
Which part of the problem you solve first depends on what we've been given.
- This being an inelastic collision problem, I'm tempted to jump straight into solving it with conservation of momentum:
That one equation has two unknowns. I could solve for the initial velocity of the bullet if I knew what the final velocity of the bullet-block mass was just after the collision. How can I figure that out?
A pendulum swinging up is a conservation of energy problem, and I have enough information to be able to solve that. So I'll do that first, and then work my way backwards from there.This "initial velocity" for the energy part of the problem is the same as the "final velocity" from the collision part of the problem. So:
- We now know the masses and velocities of the bullet and block both before and after the collision, so we should be able to use those with a conservation of energy equation to figure out what the ΔEint was.
Jane and Tarzan
Tarzan (69kg) is on the ground, about to be eaten by a tiger. Jane (62 kg) climbs 14 meters up a nearby tree and swings down towards the ground on a vine. She swings past Tarzan, grabbing him as she passes by, and they swing together up into another tree. What is the maximum height that Jane and Tarzan can reach on their upswing?
This is another classic problem because there are now three parts to the problem:
- Jane swinging down
- Jane grabbing Tarzan
- Jane and Tarzan swinging up together
Which of these are energy problems? Which of these are momentum problems?
Let's take care of the question of Jane swinging down first, and use conservation of mechanical energy to get her velocity just before she grabs Tarzan.
Now there's a collision to analyze using conservation of linear momentum:
And immediately after the collision, with their new velocity, let's see how far they can swing upwards:
Bullet and a block
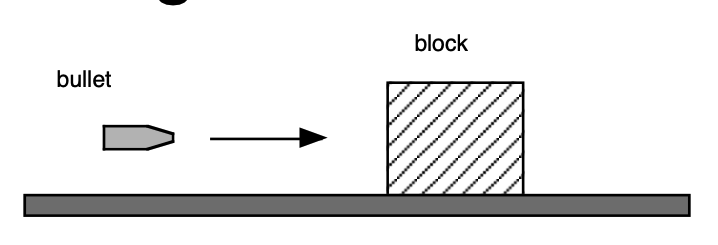
A 100 gram rubber bullet is fired horizontally at an 800 gram block of wood which is sitting on top of a flat surface. The coefficient of kinetic friction between the block of wood and the surface is 0.70, and the block slides 50 cm before coming to rest. If the bullet collided elastically with the block, what were its initial and final velocities?
This is an "elastic collision," so the first thing that might be helpful is knowing how to manipulate those equations.
Now that we know that we've that useful relationship, we can solve this problem.
First, let's use conservation of energy to figure out what the bullet-block's final velocity was just after the collision. (We could use Fnet=ma and kinematics, too.) That final velocity after the collision is also the initial velocity it had just as it started sliding across the surface.
Now, let's work backwards to see what we can discover about the collision itself.
9.4.5. Two-Dimensional Collisions
Because momentum is a vector, we need to take into account the direction of momentum, which we have been able to do up until know by considering positive and negative directions along a single axis.
If a problem occurs in 2- or 3-dimensional space, it requires considering linear momentum along those other axes as well.
Car Collision
A 1000 kg car traveling north at 4 m/s collides with a 800 kg car traveling east at 3 m/s. After the masses of the two cars have locked together, what is the final velocity of the wreckage just after the collision?
Because the two cars lock together in the collision, we take that to mean that they have a shared final velocity, making this a perfectly inelastic collision. It's occurring in 2-dimensions, however, so we'll need to solve the problems by breaking it up into components (or using i-j notation if you prefer).
In the x-direction:
And in the y-direction:
Two-dimensional elastic collisions have three equations that can be used to solve the problem:
With three equations to use, that's three unknowns that a hard problem might have you solve for, and solving those simultaneous equations is no fun.

One subset of the 2-D elastic collision problem is that of a "glancing collision," when one mass comes along to strike another identical mass that is stationary. In those situations, it can be shown that the final velocities of the two masses are at a 90-degree angle to each other.
In the situation shown here, the 5-ball is traveling in the positive-x direction at some velocity when it collides with the stationary 2-ball. The 2-ball is knocked up and to the right, and the 5-ball continues down and to the left. The angle between those two paths after the collision is 90-degrees.
The proof that this happens is more extensive than we want to go into here, but the result can be summarized in the momentum analysis here:
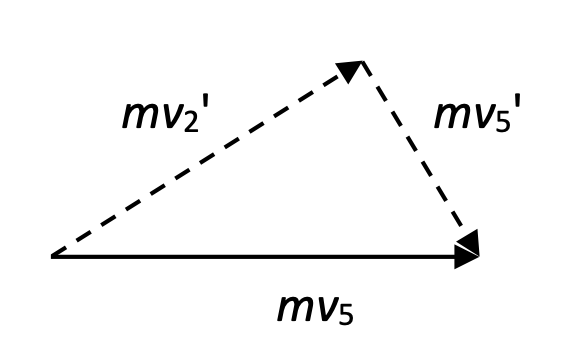
If momentum is going to be conserved, the initial momentum vector p5 will need to maintained after the collision, and we can see that p5' and p2' do indeed graphically (tip-to-tail) sum to the original vector.
Playing Pool
In the diagram shown above, the 5-ball is traveling east with an initial velocity of 1.00 m/s when it hits the 2-ball, which is knocked so that it travels at 50 degrees north of east. Assuming this is an elastic collision:
- At what angle is the 5-ball deflected after the collision?
- What are the final speeds of each ball?
- As mentioned above, the angle between the two masses after an elastic glancing collision of this type is 90-degrees. Therefore, the 5-ball is traveling at 90 - 50 = 40 degrees south of east after the collision.
- Kinetic energy is conserved, and momentum is conserved in both the x and y directions. Here's one way to solve for the final velocities, using a momentum analysis:
We can solve these simultaneous "two equations in two unknowns" now:
And substituting back in:
9.5. Center of Mass
Most people have something of an intuitive idea of where the center-of-mass of an object is. Maybe it's as simple as "the point where you'd put your finger if you wanted to balance a softball bat across it."

Where would you place your finger along the length of the bat so that it balances?
It's important to note right away that the center of mass is not a position at which there is equal mass on either side. In the example shown below, there are just two masses attached to a stick of negligible mass. There is much more mass on the left side, but its position is closer is closer to the center-of-mass as well. There is less mass on the right side, but it is located farther away. Both masses end up having the same "leverage" on the stick.
Center of Mass
The center-of-mass is located at the "weighted average position of the system's mass."

A force F applied at the center of mass of a system of total mass m will cause it to accelerate in the direction of F, without rotation.
Let's try that with some numbers.
Calculating center of mass
In the diagram above, the blue cylinder has a mass of 3m and the red cylinder has a mass of 1m. The two masses are attached to a thin light rod so that they are 1.0 meters apart. Calculate the center of mass of the system.
With masses distributed along a line, a one-dimensional arrangement, its easy to calculate the center-of-mass. It's almost as easy to calculate the center of mass for a two-dimensional arrangement of masses, or even a three-dimensional arrangement of masses. There are a few ways that you can express these two- and three-dimensional relationships.
Center of Mass in 2- and 3-dimensions
We can express these individual components as a multi-dimensional r vector as well.
Two-dimensional center of mass, #1
A 2 kg mass is located at position (2,3), and a 4 kg mass is located at position (-2,-1). Sketch this two-mass system, and calculate the position of its center of mass.
Two-dimensional center of mass, #2
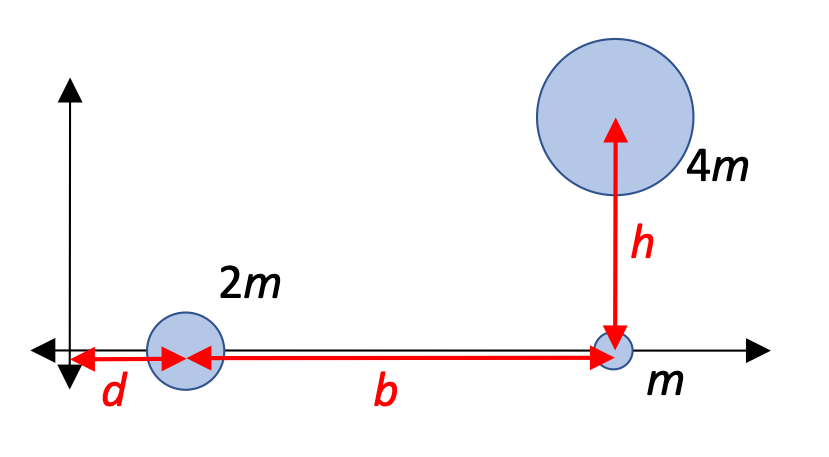
Calculate the position of the center of mass for this arrangement of particles of mass m, 2m, and 4m.
Let's take a look at the x-component of the center-of-mass first:
And for the y-component:
9.5.1. Continuous distribution of Mass
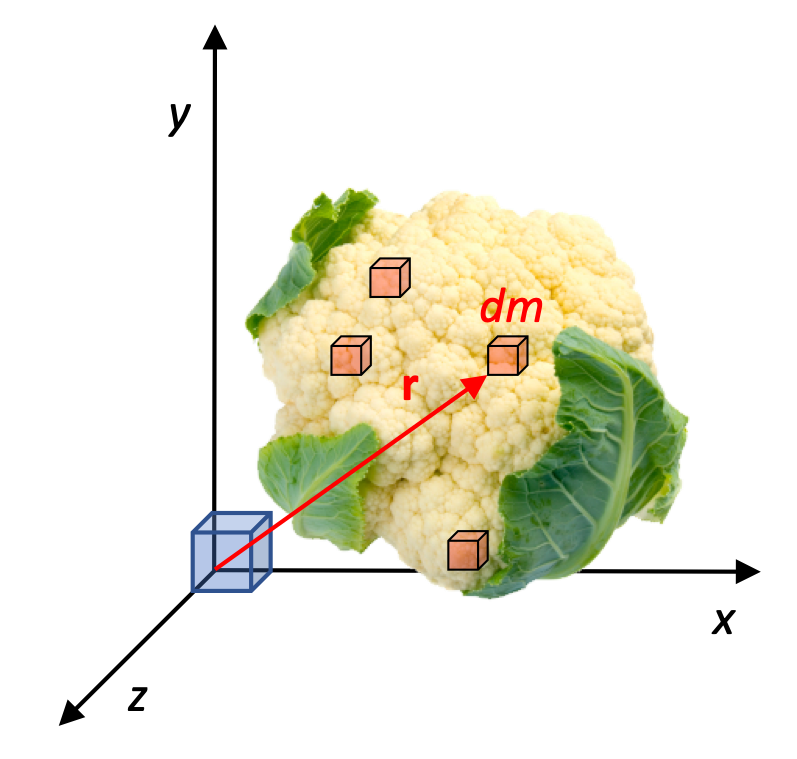
Locating the center of mass for a large, extended object can be a little trickier, but the same basic principles apply: large objects have lots of particles, all located various distances from the center-of-mass cm.
For these continuous distributions, we're going to need to use integrals to add up the effects of every little small mass dm. The position r of that mass is going to be a factor as well, of course.
Single-variable limitations
Because r is a vector, potentially in 2- or 3-dimensions, and because this course only requires single-variable calculus, we will be somewhat restricted in the geometries of objects that we can analyze.
For these larger distributions of mass, consider the total mass to consist of a series of discrete Δm chunks. We can figure out the x-component of the center-of-mass by summing the weighted-position of those masses. Better, we can let the size of those Δm chunks approach 0, at which point we can express this analysis in integral form:
In other dimensions:
Taking a look at these integrals, you can see that we have an issue. Consider the ycm integral, for example. We can't integrate a y-based function with respect to m. They're not directly related to each other.
We can, however, use density to create functions that we can analyze.
Let's see how to do that!
9.5.1.1. Density
For these analyses, we’re going to need some way of relating dm to the location of that mass. We can do this by considering either:
- the linear density λ ("lambda") for linear situations (like a long, thin, rod)
- the surface area density σ ("sigma") for surface-based analyses, or
- the volume density ρ ("rho") of the object for volume-based analyses.
You're almost certainly aware of "volume density," where Density = mass divided by volume:
This works for the overall density of a volume, but we can also consider the very small mass of a very small Volume of that larger mass:
We can also express this relationship in a slightly different way:
With this new relationship between dm and dV we can solve the integrals shown above. We'll see how to do that in just a moment.
Continuous distributions of mass and density
For a given axis:
For substituting into the integral to solve for center of mass:
Let's solve some problems.
Long, thin, uniform, rod

Assuming that a long, thin, rod has a uniform linear density λ, show that the center of mass for the rod is in the middle.
We already know that the center of mass for a uniform rod is in the middle of the length of that rod, but let's use this opportunity to practice using the integral.
Long, thin, rod with changing density
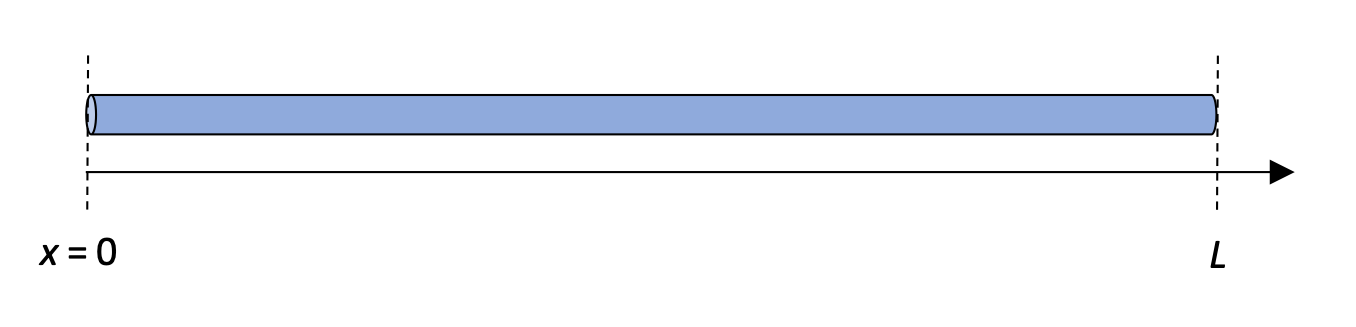
Assuming that a long, thin, rod has a changing linear density λ = α x, where α is a positive constant, calculate the location of the center of mass.
This rod is a little more interesting. At x = 0 the rod has a mass of dm = α dx = 0 kg, while at the end L it has a dm based on a linearly-increasing density.
Let's solve that integral:
This is fine so far, but... we don't know the mass M. How can determine that value?
Substituting back in:
For a mostly linear object like a baseball bat or a long, thin rod, we can think of the center-of-mass as being that location where, if we were to put our finger there, the object would balance, with gravity having an equal effect on either side of the object.
In a similar way, with a 2-dimensional object like the triangle in the next problem, we can imagine attaching a string to the 2-dimensional surface. If we attach that string at the center-of-mass in both the x and y directions, the triangle will maintain a horizontal position as we support it. If we attach the string at any other location, the forces acting on it will supply uneven torque effects, causing the triangle to hang to one side.

A triangle
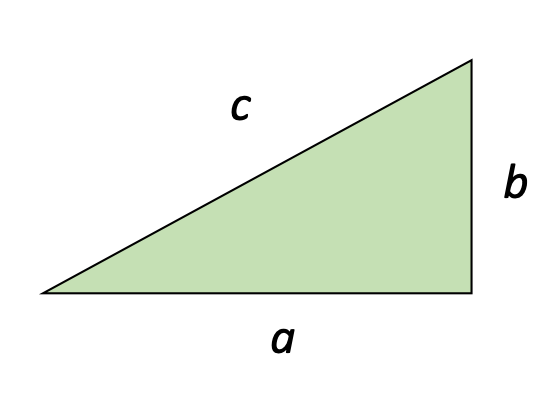
Find the center of mass of the 2-d right triangle shown here. The triangle has a constant thickness and density.
This is an interesting problem, because we need to use the integral to calculate center-of-mass twice, once in the x direction and once in the y direction. Let's focus on the x direction, and because we're working with an area, we'll use the "surface density" form of the integral:
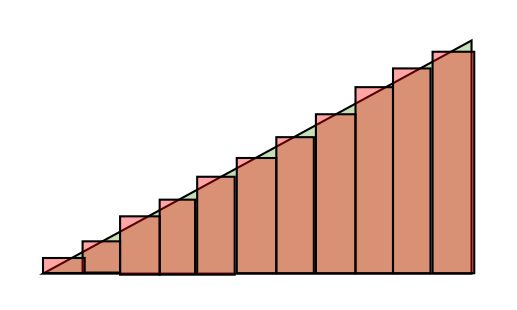
This is awkward. We're trying to integrate x with respect to area A? Where is dA? How is it related to x?
The dA refers to each of the rectangles shown here that, taken together, over the entire area of the triangle. Each of those rectangles has a width dx, and a height y related to the value of x.
Related how? The hypotenuse of the triangle follows the function y = mx, where m = the slope of the line, b/a. Let's put that all together.
Substituting this into our center-of-mass integral:
This is pretty good, but let's again see if we can simply things by calculating the mass of the triangle:
The conclusion is that the center-of-mass along the x-axis is 2/3 away from the "skinny" end. We can extrapolate that result to identify the center-of-mass along the y-axis, also 2/3 away from the "skinny" end of the triangle.
9.5.2. A System in Motion
Now that we know a little about center-of-mass for objects and systems, let's do a derivation in which we take time time-derivative of a center of mass.
The time-derivative of position is velocity, so
All of these mv values are the individual momentums of each component of the system. Let's rearrange the equation a little:
This is an interesting result because it reveals that the total momentum of a system of moving particles is the same as the momentum of the center-of-mass of that system. This remains true even if the velocities of the individual particles are moving in different directions (as long as their is no external Force providing an impulse to the system).
This animation from The Mechanical Universe demonstrates the effect nicely.
Ice hockey is dangerous
A hockey puck of mass m is moving at 10 m/s in the +x direction when it explodes into two pieces, one of them with mass m/3 traveling in the +x direction at 15m/s.
- What is the velocity of the second piece after the explosion?
- Where is the center of mass of the system 3.0 seconds after the explosion?
- We can solve for the final velocity of the second piece simply by using conservation of momentum. This is effectively a "recoil" problem, except that the system is moving when the two pieces come apart:
- 3.0 seconds after the explosion we have two ways that we can identify the location of the center-of-mass. The simplest is to realize that the explosion doesn't affect the velocity of the center-of-mass. If it was moving at 10 m/s in the +x direction before the explosion, it will continue to move at that rate after the collision. Therefore:
It's a little more tedious, but perhaps useful to take a look at the individual positions of the two masses 3.0 seconds later, and determine the center-of-mass based on those values:
They're the same!
There is one more interesting derivation that we can perform here. We have determined that the total momentum of a system is equal to the momentum of its center of mass:
What happens if we take the time-derivative of that equation?
This is Newton's Second Law of Motion!
It's actually a slightly different form from the original. Our original Fnet = ma applied a particle of mass m. Here, we have arrived at an equation that justifies our application of the Second Law to a larger system of particles. Applying a net Force to the center-of-mass of that system will cause it to accelerate linearly, just as if it were a single particle.