Chapter 8: Potential Energy & Conservation of Energy

8.0. Overview

Now that we know a little about Work, and have developed the concepts of kinetic energy, potential energy, and conservative and non-conservative forces, we can put these pieces together to answer some serious questions.

Let's get started!

  1. Potential Energy
  2. Conservative Forces
  3. Conservation of Energy definition
  4. Problem Examples
  5. More on Potential Energy

8.1. Potential Energy

Potential Energy can be characterized as energy "stored" in a system that can be released or converted to another form later on.

In this course we will restrict ourselves to thinking about only two kinds of potential energy:

Gravitational potential energy Ug is the energy stored in the gravitational field between two masses, a skydiver in Earth's gravity field, for example. When the skydiver jumps from a plane, her stored potential energy in the field is converted to kinetic energy.

Elastic potential energy Us is the energy stored in a system with a spring in it, a slingshot that has been stretched out, for example. When the system is released, the stored energy in the elastic band is converted to kinetic energy.

 

Most people find the idea of "stored" energy intuitive, but it's going to require that we clarify our thinking on Work and energy. In particular, if we're going to think about systems as having potential energy, we need to reconsider how we talk about the Work done by gravity and by springs.

8.1.1. Rethinking Work done by Gravity

8.1.2. Derivation for Gravitational Potential Energy

8.1.3. Derivation for Elastic Potential Energy

8.1.4. Some important details

At this point we've defined two types of potential energy:

When working with potential energies, keep in mind the following:

That "negative change in potential energy" may seem odd, but again, when (positive) Work is done by a gravity field or a spring force, the potential energy is decreased. That's why the signs of the two sides of the equation are different.

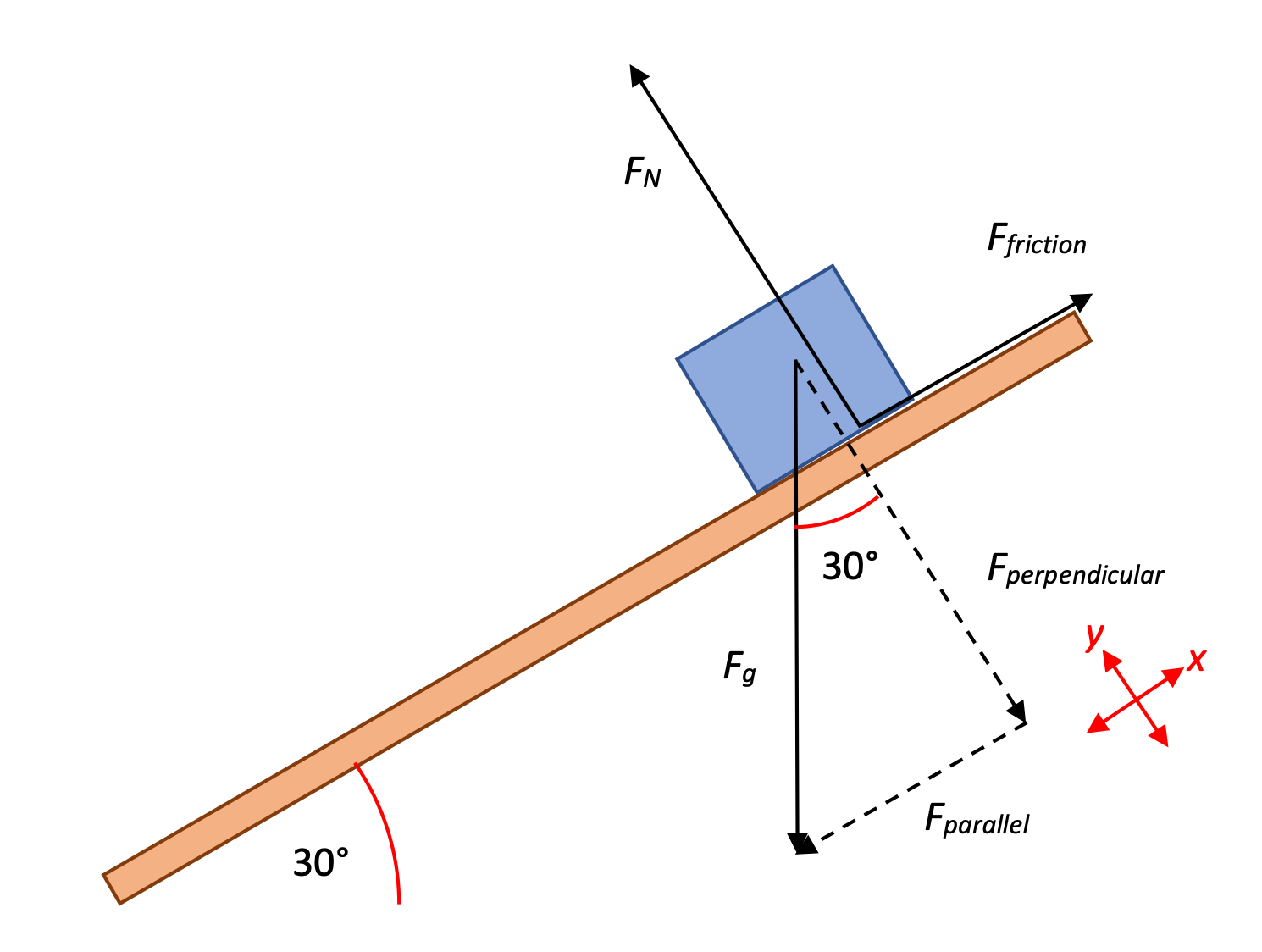
8.2. Conservative Forces

A force is conservative if work it does on a particle moving between any 2 points is independent of the path taken by the particle.

The common conservative forces that we deal with in here are the gravitational force Fg and the force exerted by a spring Fs.

Also, work done by a conservative force exerted on a particle moving through any closed path is 0.

Work done by a conservative force

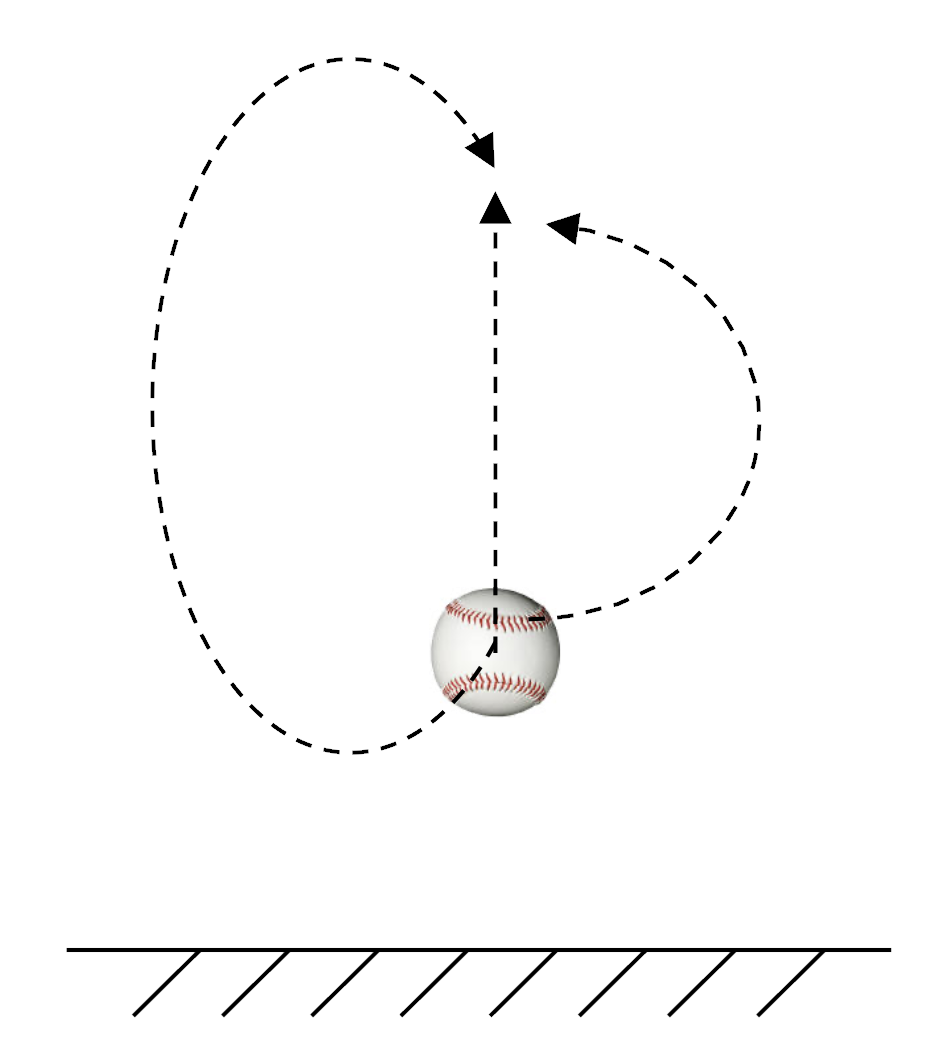
The diagram here shows a baseball being lifted up against the force of gravity in three different ways. In each case, the ball travels a different distance as it is moved. For which path is the Work done by gravity greatest?

Solution:

It turns out that the Work done by gravity is the same in each case, regardless of the path. Why is that?

When the baseball is lifted up against gravity, gravity is doing negative Work on the ball. When the ball is lowered down, gravity is doing positive Work on the ball. Regardless of how many times the ball is raised and lowered, the net result of all those Works will the be same as if the ball was simply moved from one vertical position to another.

What about when the ball has a sideways component of movement? Remember that moving sideways in the gravity field doesn't require any Work against gravity—the sideways aspects of the ball's motion don't change how much Work gravity is doing on the ball.

Here we are analyzing the motion of a mass in a gravity field, but the same analysis holds true for a mass attached to the end of a spring: the net Work done by the spring is independent of how many times the mass is moved back and forth. It only depends on the initial and final positions of the mass.

8.2.1. Nonconservative Forces

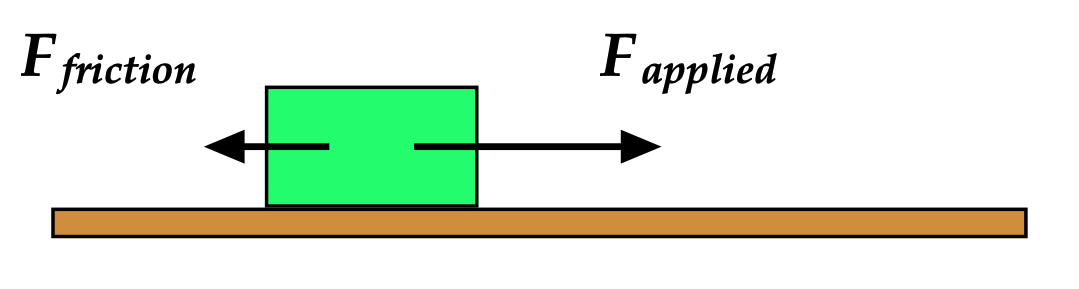
A force is "nonconservative" if it causes a change in mechanical energy, ie. net work does have to be done on an object to return it to its same location and state of motion.

The force of friction is a good example. If the block on the surface shown here slides to the right, the force of kinetic friction does negative Work on the system (with a force in the opposite direction of the block's displacement). If the block then slides back to the left, returning to its original position, friction again does negative work on the system.

The net Work done doesn't add up to 0 in moving the block back and forth. We just have more energy converted to heat. Because of this, the friction force is a non-conservative force.

Energy changes due to kinetic friction

When the force of kinetic friction acts on a moving body, the Work by that force is negative, ie. energy is removed from the system as a result.

People describe this change in energy in a variety of ways: "Energy is 'lost' from the system." "Mechanical energy is decreased due to friction." "Energy is 'converted to heat.'" Not all of these are good ways to describe what's really going on.

Perhaps the best way to describe the energy changes due to kinetic friction in a system is this:

When there is a force of friction present in a problem, there is loss of mechanical energy, and an increase in the internal energy of the system. "Internal energy" here refers to the random motion of the molecules in the system, non-mechanical energy that (usually) can't be recaptured and used.

8.3. Conservation of Energy

We've taken a look now at a number of types of energy: kinetic energy K, gravitational potential energy Ug, and elastic potential energy Us. Collectively, these energies are known as "mechanical energy," and if you ever to calculate the "total mechanical energy" of a system, you can simply add those values together.

In an "isolated system"—one in which objects in the system interact with each other only through conservative forces—the total mechanical energy of the system will remain constant, even as individual values of those energies change.

Conservation of Mechanical Energy

It has been determined through experimentation that the total mechanical energy of a system remains constant in any isolated system of objects that interact only through conservative forces.

Dropping a ball

A ball of mass m is dropped from a height h above the ground.

  1. What is the speed of the ball at a height y above the ground? (Air resistance is negligible.)
  2. What is the speed of the ball at a height y above the ground if it is given an initial speed vi at the initial height h?

Solution:

  1. Although we could easily solve this using kinematics, let's use conservation of energy to find the solution. We know that gravitational potential energy Ug is changing in this problem, and that kinetic energy K is part of the situation. So let's set up an equation that summarizes the initial and final values of those two quantities:
    Although we can select any height to be our origin (= 0) for a problem, it's often convenient and intuitive to consider the ground to be at a height of 0. With that in mind, we can expand the equation:
  2. This is an interesting variation because you might well ask, "Well, which direction is that initial speed pointing? Because if it's straight up, that's going to give a different result from a sideways velocity, or a downwards velocity."
    It turns out that the answer is the same, regardless of which direction we throw the ball.

Speed of a pendulum bob

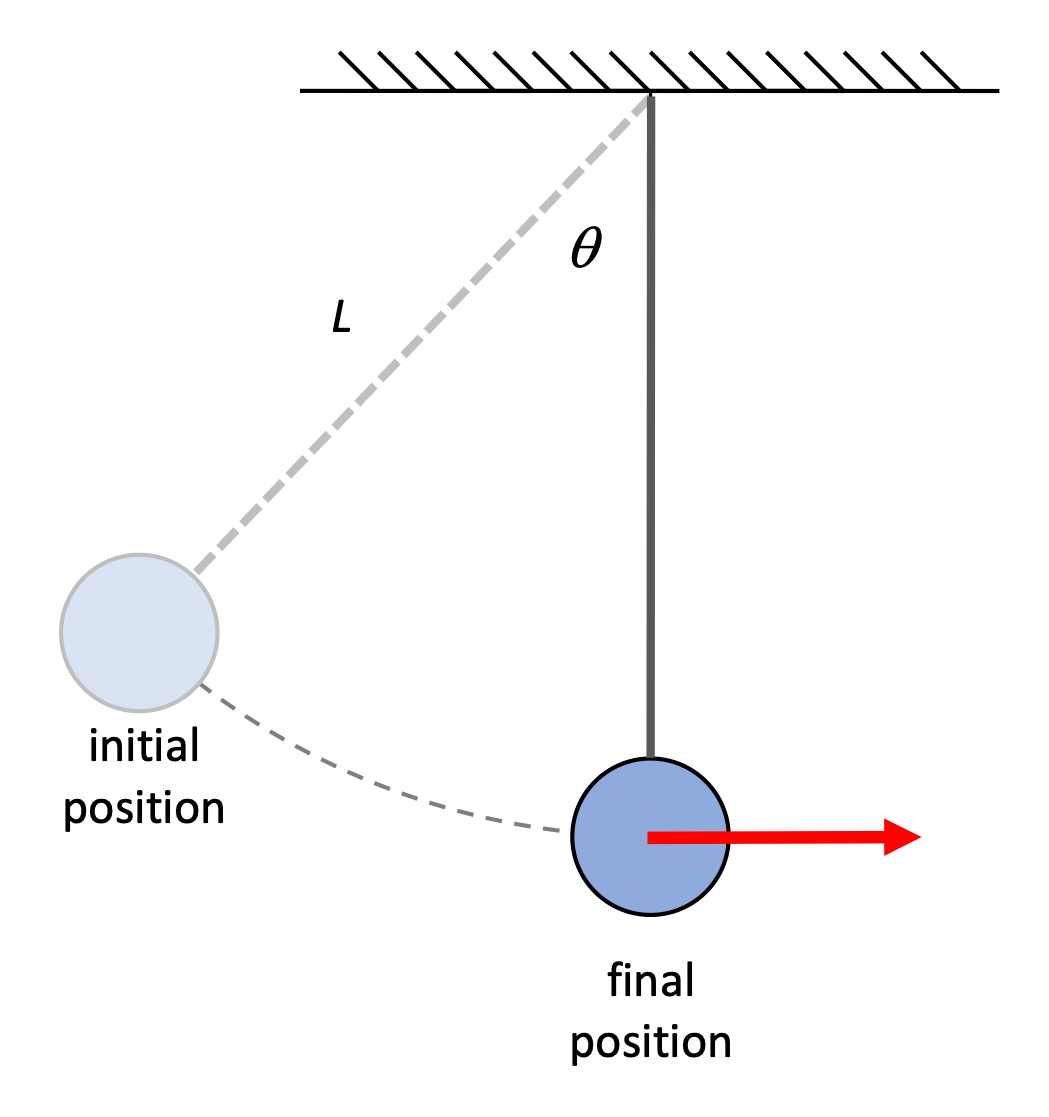
A pendulum is made of a light string of length L, with a bob of mass m at its end, is released from an angle θ relative to the vertical, as shown.

  1. Find the speed of the pendulum at its lowest point.
  2. Calculate the tension T in the string when the mass is at this lowest point.

Solution:

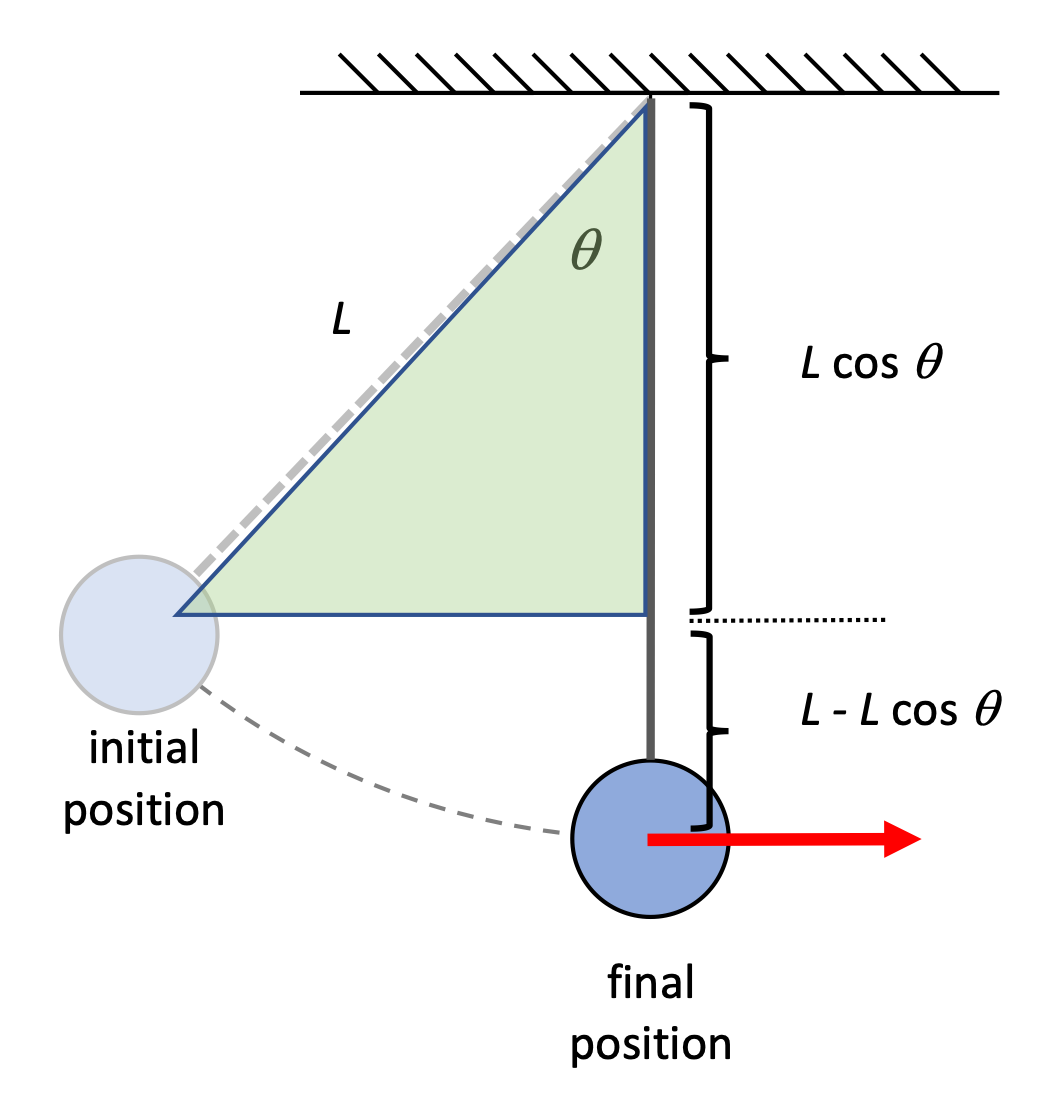
  1. This is a problem that we would not be able to easily solve using Fnet = ma because the acceleration of the bob keeps changing as it falls. If we recognize that conservation of energy is a better strategy for solving this problem, then all we need to do is figure out the initial height of the mass. The initial velocity is 0, and take the bottom of the bob's arc to be at a height of 0... what is the initial height of the bob? Knowing L and θ we can construct a triangle and identify the length of the vertical side. This reveals that the initial height of the bob is L - L cos θ. And so:
  2. The tension at the bottom of the swing is a force, so we'll need to turn to an analysis that uses Fnet = ma. In this case, the mass is swinging in a circle, so we'll do a centripetal analysis, and our free-body diagram will include two forces acting on the mass: tension T up and Fg down.

8.3.1. Non-isolated systems

It is also possible to look at non-isolated systems in which Work from an external force changes the energy of the system, or a non-conservative force (such as friction) reduces the total energy of the system.

In the picture here, a boy is pushing a girl on a swing. The work he does in applying a force over a distance adds energy to the "pendulum," causing her to swing higher and higher.

There are other non-conservative forces at play in this situation as well. A force of air friction acting on the girl as she swings, and the force of sliding friction at the squeaky attachment at the top of the swing both transfer mechanical energy out of the system, converting it to "thermal energy," the random motion of molecules in the air and the material of the swing that dissipates the mechanical energy.

In these non-isolated systems, even if mechanical energy is not conserved, total energy is. By carefully accounting for all the energies present in the system, we can solve some very interesting problems.

 

Conservation of Energy

More generally speaking, energy, in all its forms, is always conserved.

Note that there are a number of other ways that the energy of a system may be altered, including heat Q that flows into or out of a system, mechanical waves, matter transfer, electrical transmission, electromagnetic radiation... These more exotic forms of energy transfer are not covered in this introductory course.

8.4. Problem Examples

Let's take a look at the variety of problems we can solve using an analysis that uses Conservation of Energy.

Problem-solving strategy for Energy problems

  1. Identify problem as using an Energy analysis.
  2. Define your system: Identify initial and final positions for all objects.
  3. Select zero reference points for all potential energies.
  4. If any type of friction is present, mechanical energy will not be constant; account for friction using
  5. Write equation with all energies present, and solve for unknown.

Kid on a slide

A child of mass m, starting from rest slides down a playground slide which starts at 6.00 m above the ground.

  1. Find vfinal assuming she slides with no friction.
  2. Find how much energy is "lost" to friction if her final velocity at the bottom is 8.00 m/s and her mass is 20.0 kg.
  3. Find the coefficient of kinetic friction from the previous problem if the slide angle is 30 degrees above the horizontal.

Solution:

  1. Draw a picture of the slide, and consider the bottom of the slide to be at height h = 0. Because there is no energy converted to heat in this process, we can use Conservation of Mechanical Energy to solve.
  2. The child is not traveling as fast as we calculated above, so it's clear that a friction force is removing energy from the system, converting it to heat, or "thermal energy": the random kinetic energy of the particles in the kid and the slide surface is a little greater than it was before—the temperature of those objects has increased a little.
    How much energy was converted, though?
  3. The coefficient of kinetic friction is determined using , so we'll need to identify what those forces are. Any problem that involves forces should include in its solution a free-body diagram to identify how those forces are being determined.

Block pulled along a surface w/ friction

A 6.0-kg mass, starting at rest, is pulled with a constant horizontal Force of 12.0-N for a distance of 3.0-m on a rough surface with μk = 0.15. Find the final speed of the block using a Work-Energy analysis.

Solution:

In this problem the constant force on the block accelerates it from rest. We could solve this problem using Fnet = ma, but we'd have to do a free-body diagram, and we've have to figure out the net force, and then figure out the acceleration, and then we'd have to get a kinematics equation to solve for final velocity... There are a lot of places where we could make mistakes along there. We could do it, though.

But let's use Work-Energy, as the problem suggests. What kinds of energy and/or work do we need to account for in this problem? Do we see those energies at the beginning or at the end of the problem?

Car skidding on a road

A car traveling at an initial speed v locks up its brakes and skids a distance d as it comes to a halt.

  1. How far will it skid if its initial velocity is 2v?
  2. What happens to the car's kinetic energy K as it skids to a stop?

Solution:

  1. In order to determine how far the car is going to skid under the new conditions (twice the velocity), we need to first understand what the relationship is between the original velocity and the skid distance. Let's set up an energy equation with the relevant variables, and solve to see how distance depends on v. We see that distance d (or x) is proportional to the square of v. Thus, if v increases by a factor of 2, the distance d will increase by a factor of 22, or 4. The car will take four times the distance to come to a halt.
  2. The car's kinetic energy is converted to thermal energy, or ΔEint. This energy appears as a rise in temperature of the tires and the road, as the random kinetic energy of the particles in those materials is increased.

Mass attached to a horizontal spring

A 1.6 kg block is attached to a horizontal spring with k = 1.0 × 103 N/m.The spring is compressed 2.0 cm and released.

  1. What is the speed of the block as it passes through the equilibrium position? (Assume frictionless.)
  2. What is the speed of the block as it passes the equilibrium position if there is a constant friction force of 4.0 N retarding its motion?

Solution:

  1. 0.5 m/s
  2. 0.39 m/s

Masses, pulley, and friction

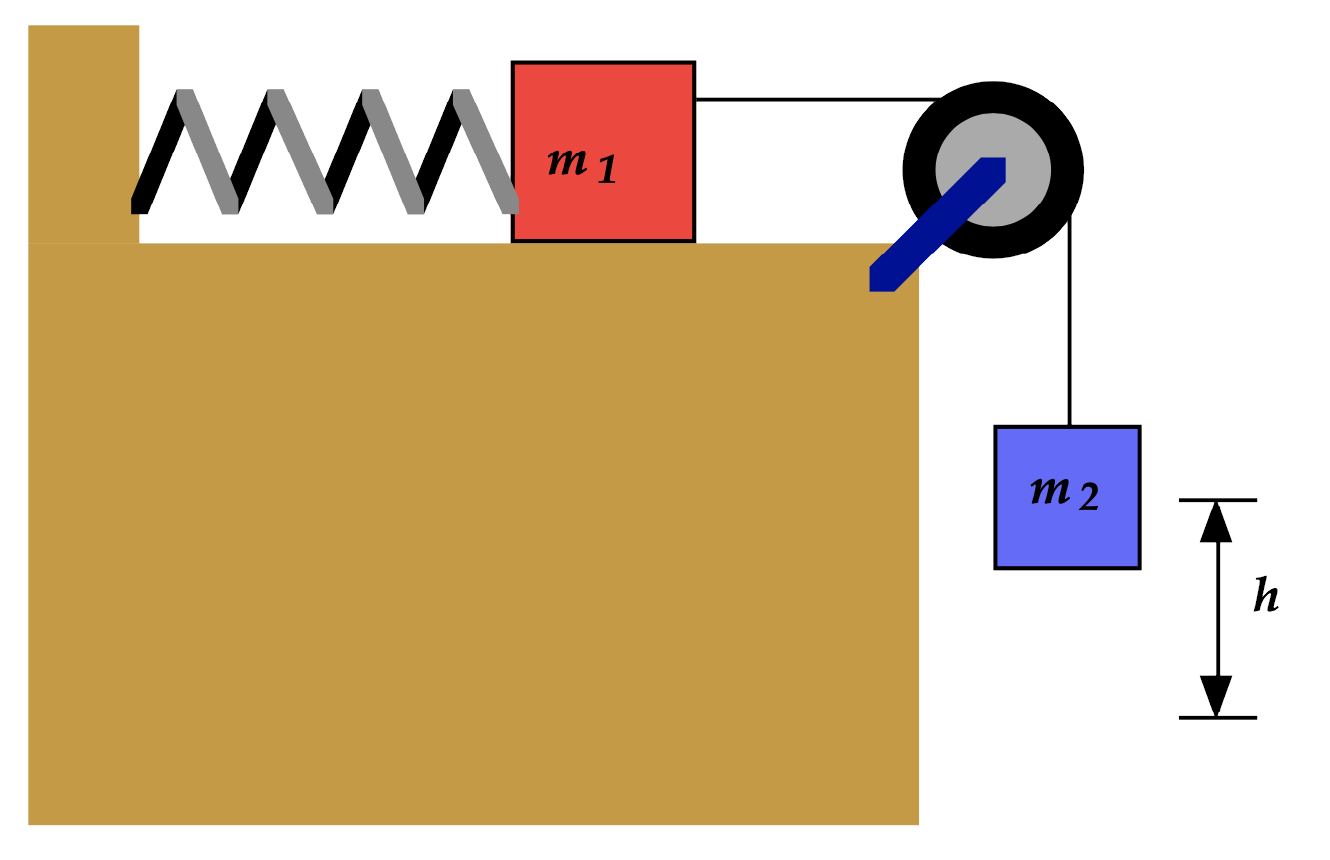
Two blocks are connected as shown. Spring starts uncompressed. When m2 is released, it slowly descends a distance h before coming to rest. Calculate μk between m1 and surface.

Solution:

Energy and a vertical spring

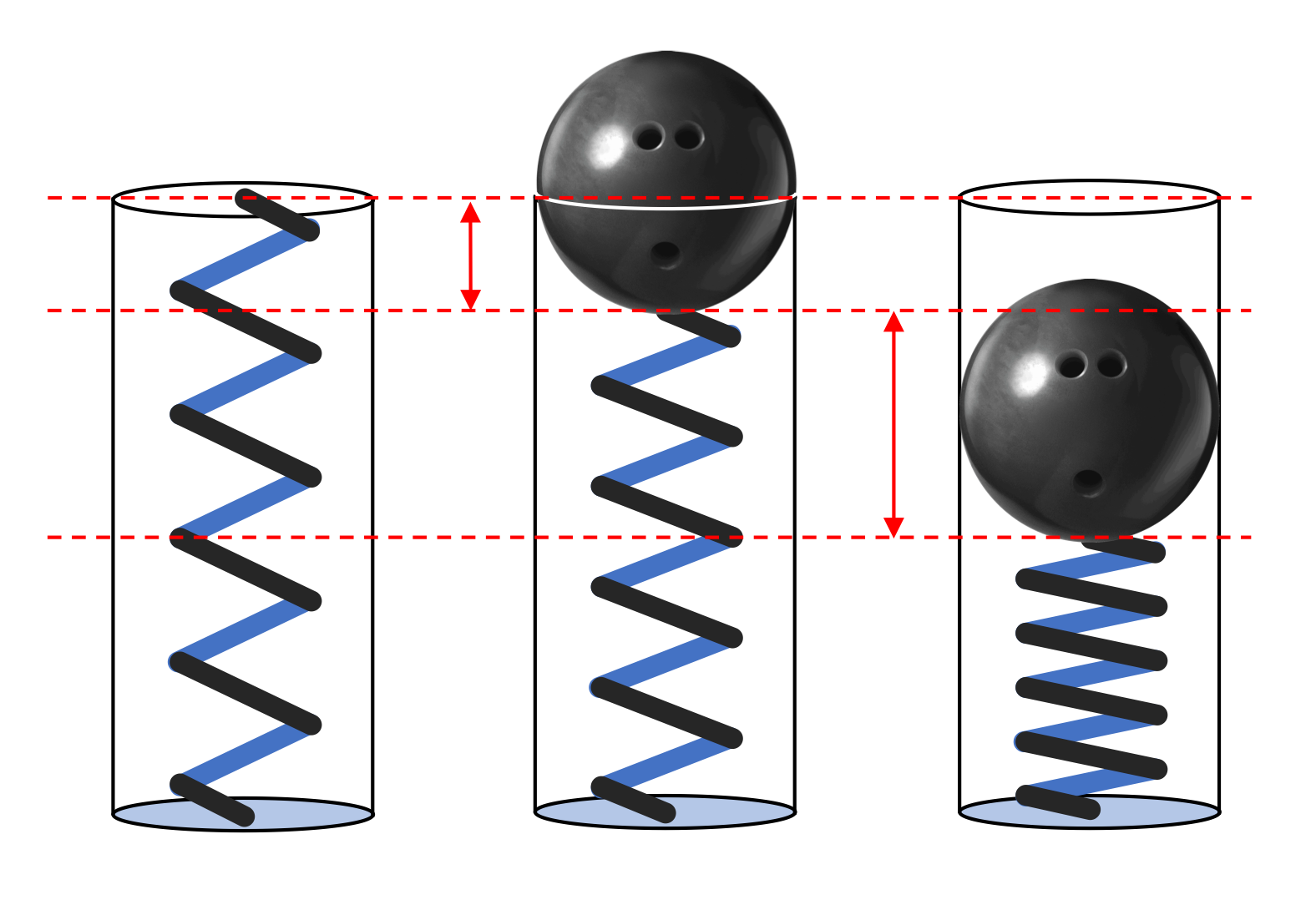
A spring-based cannon is constructed as shown, with a smooth vertical tube and a spring that, in its uncompressed position, just reaches the top of the tube. The spring has a spring constant of k = 120 N/m.

  1. A 2.00 kg bowling ball is gently placed on top of the spring and allowed to lower down into the tube where it comes to rest on the spring. How far has the spring compressed?
  2. A mechanism allows us to pull the bowling ball even farther down into the tube, compressing the spring another 50 centimeters. How much potential energy is stored in the spring?
  3. The ball is released. How fast is it traveling when it reaches the position from part (a)?
  4. What is the maximum height above the top of the cannon that the bowling ball reaches?

Solution:

  1. The spring is compressed to the position where its force upwards is balanced by the force of gravity pulling downwards on the ball. At this position, the ball is in equilibrium.
  2. With the bowling ball resting on the spring, its potential energy in the spring is calculated based on its displacement from the uncompressed position (at the top):
  3. The potential energy of spring-ball system is converted to kinetic energy K, so
  4. The elastic potential energy is converted to gravitational potential energy. Although the ball is moving as it travels, at the initial and final positions it has an instantaneous velocity of 0, so:

8.5. More on Potential Energy

There are a couple of more important aspects of Potential Energy that we need to look at.

8.5.1. Conservative Forces and Potential Energy

We've already defined potential energy functions for the force of gravity (a conservative force) and for the force of a spring (also a conservative force). In fact, Potential Energy functions can only be defined for Conservative Forces.

Conservative Force and Potential Energy

There are a number of ways of relating the Work done by a conservative force and potential energy.

Again, we see that Work done by a conservative force reduces the potential energy of the system.

Instead of integrating Force along the displacement, we can take a look at the small change in potential energy dU as the conservative force acts over a small displacement dx. Expressing this as a differential, we see that:

This interesting result reveals that we can identify a conservative Force by:

  1. taking the derivative of a potential energy function with respect to position, or
  2. looking at the slope of a potential energy vs position graph

Calculating the Force of a spring

Given that the potential energy function for a spring is , calculate the conservative force Fspring.

Solution:

Differentiating the function:

It's delighting in some ways to see Hooke's Law emerging from this analysis, but we shouldn't be too surprised: Hooke's Law is what we integrated in the first place to produce the potential energy function!

8.5.2. Potential Energy Diagrams

Finally, let's take a look at potential energy diagrams, in which a potential energy function is graphed vs. the displacement of the system.

Take a look at this graph of the function .

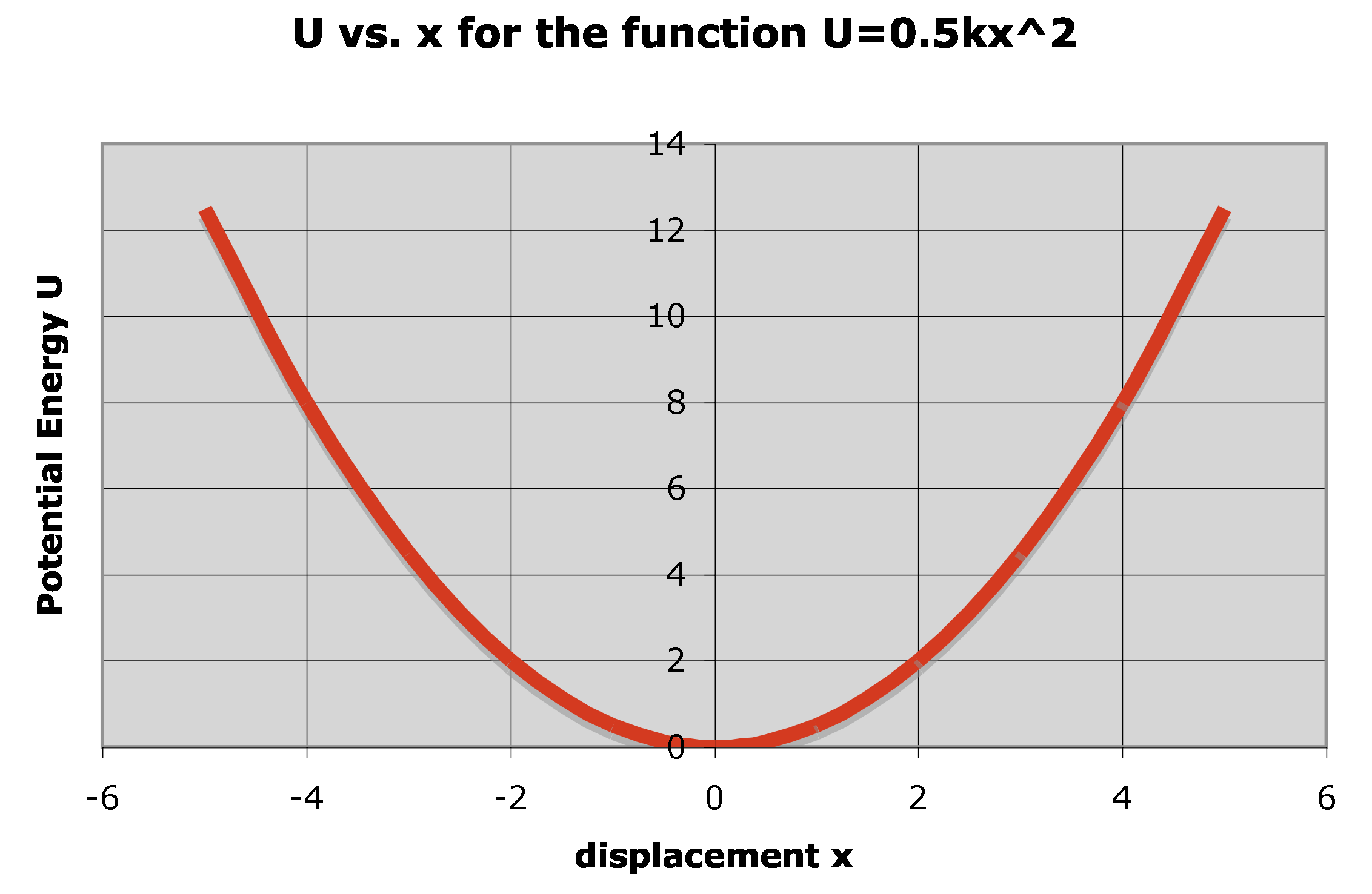
As mentioned above, the slope of a Potential energy-displacement graph is associated with a conservative force, both its magnitude and direction.

Here, if we consider the bottom of the curve, where x = 0, the slope of the function at that point is 0. This suggests that there is no force acting on the system while it is in this state.

This function could represent a variety of systems. We're certainly already familiar with a mass-spring system, and with that context, we can see that the mass-spring system, if the mass hasn't been displaced, is at equilibrium position... the position where there is no Force from the spring.

What happens if we displace our mass a little to the right, in the +x direction? From the context of the mass-spring system, we know that the spring starts to pull back to the left, exerting a "restoring force" that tries to return the system toward that point of equilibrium.

From the more general context of the potential energy diagram, the curve over in the x > 0 region has a positive slope... and F = -dU/dx: the Force for this system is acting in the negative direction, just as we intuited from the mass-spring system.

Whether it's a mass-spring system that we're looking at or any other function that follows the F = -kx relationship, this potential energy diagram can be used to help understand the behavior of that system.

Stable equilibrium

Question: What happens if we displace the system in the -x direction? Which direction does the Force act then?

As the graph ascends in the x < 0 part of the graph, it has a negative slope, implying the the Force will be in the positive direction, again, trying to return the system toward equilibrium.

Because the force is for this function is always trying to restore toward the equilibrium position, that position is referred to as a point of stable equilibrium.

There are some other interesting behaviors to consider.

Conservation of Energy

Question: What happens if we displace the system in either direction and release it? How does the system behave over a period of time?

If we displace the system toward the negative side and release it, it begins with an initial mechanical energy of U. As the system moves toward equilibrium, U decreases, but the kinetic energy of the system increases. At the bottom of the curve, there is no more potential energy U: it has all been converted to kinetic energy K.

The system doesn't stop there, of course. The kinetic energy of the system carries its state past the equilibrium position and on into the positive range of the graph. K diminishes, converted to potential energy U as we climb the right side of the curve. At its "highest" position, all of the K has been converted back into potential energy U... and the process continues from there.

It could be a mass attached to a spring (oscillating back and forth), it could be a marble in a glass bowl, it could be an atomic bond, or simply an abstract function. In all of these cases, we can use the potential energy diagram to understand the concepts of conservative forces and displacements of the system.

[Pro Tip: it helps to visualize the potential energy diagram as a "marble in a bowl," or in more complex situations, a "marble on a line."]

Unstable equilibrium

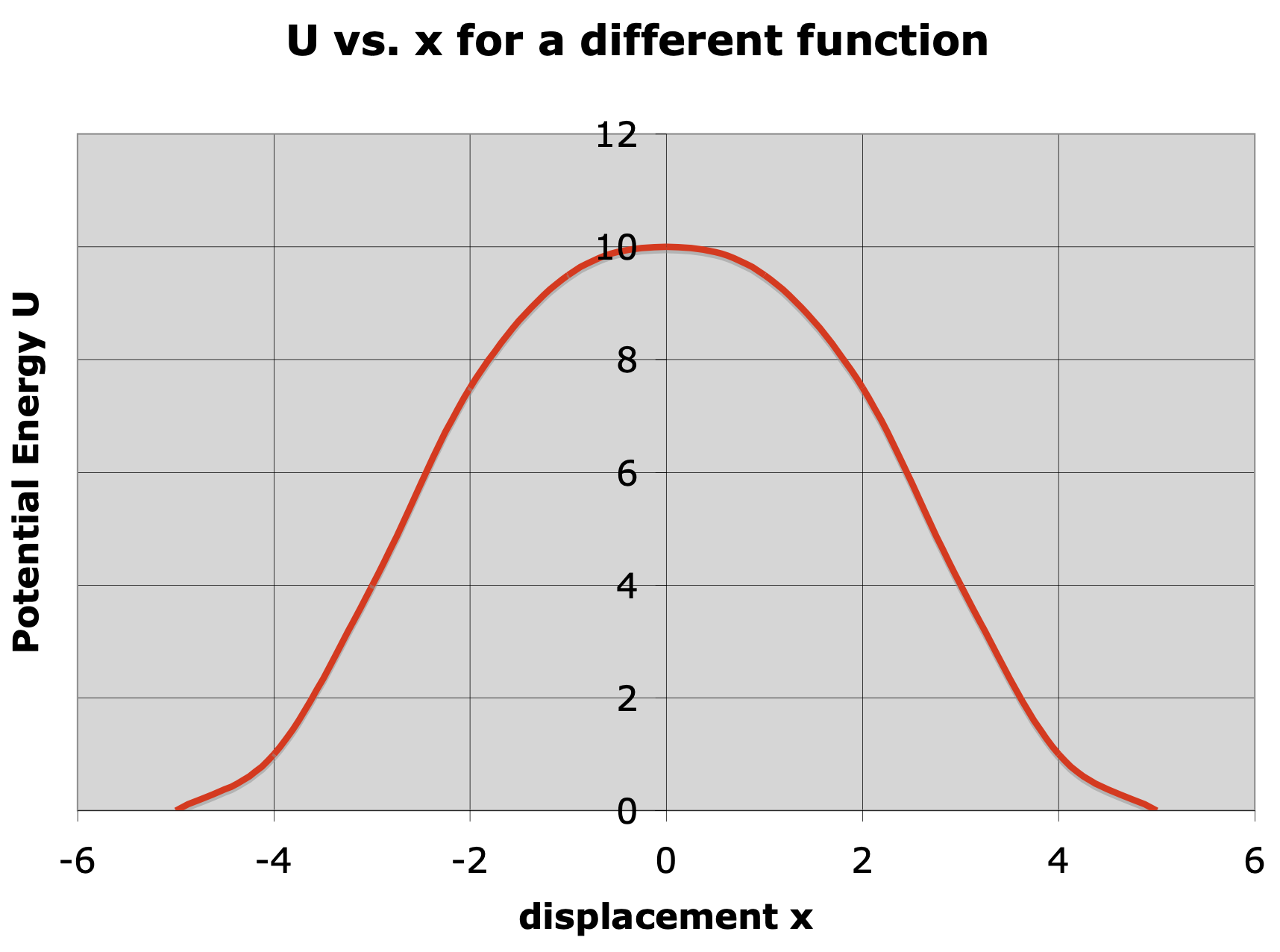
Question: This potential energy function also has an equilibrium position in it, but it's a point of "unstable equilibrium." Why? And what are some other similarities/differences between this function and the previous one?

Let's see what this all looks like in the context of an AP problem!

Answers:

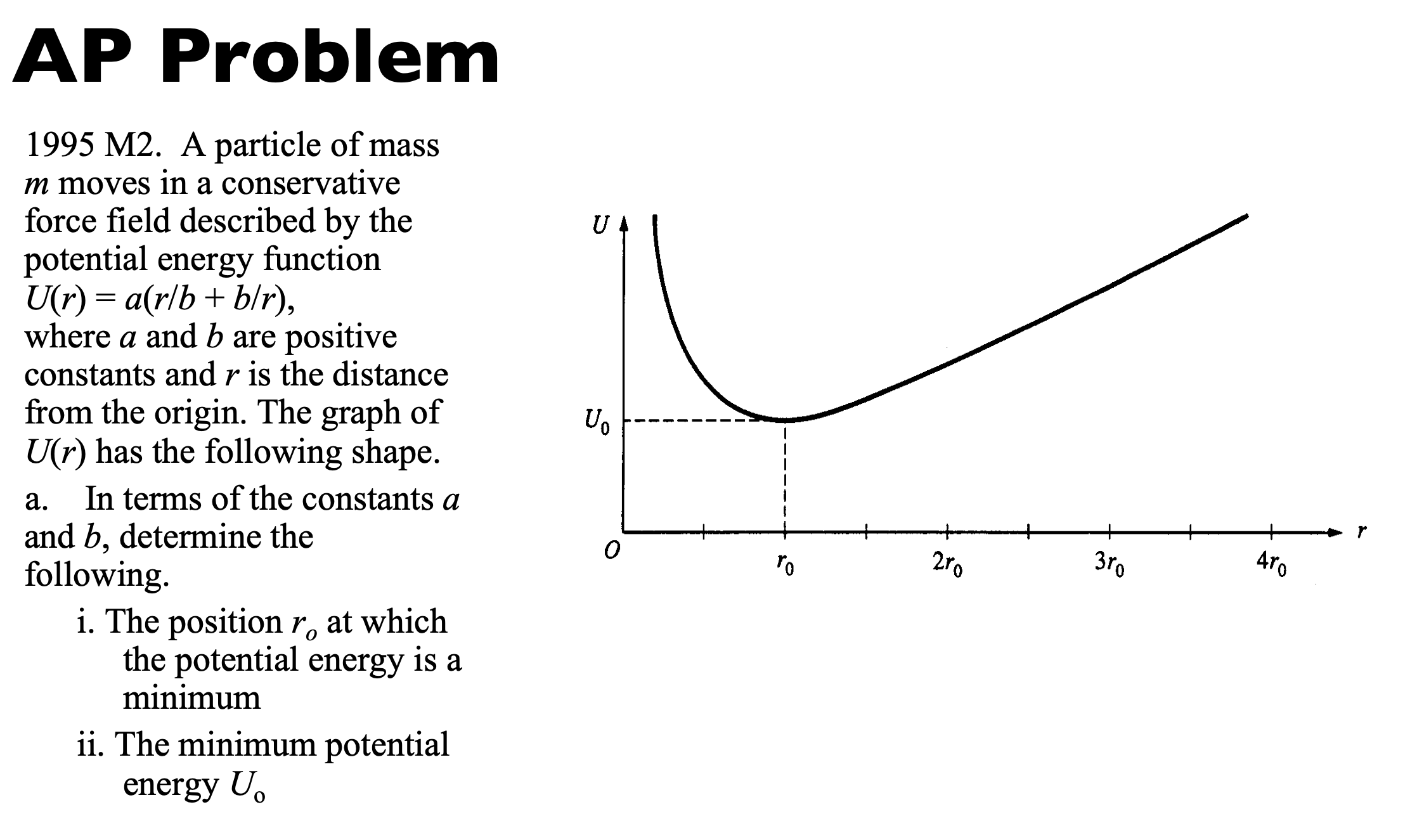
  1. i. Potential energy is at a minimum, a point of stable equilibrium. F = -dU/dr, and F = 0 at that minimum. Take the negative derivative of the given potential energy function and solve with F = 0 for r to get r0 = b
    ii. Solve back into the original potential energy function to get U0 = 2a

Answers:

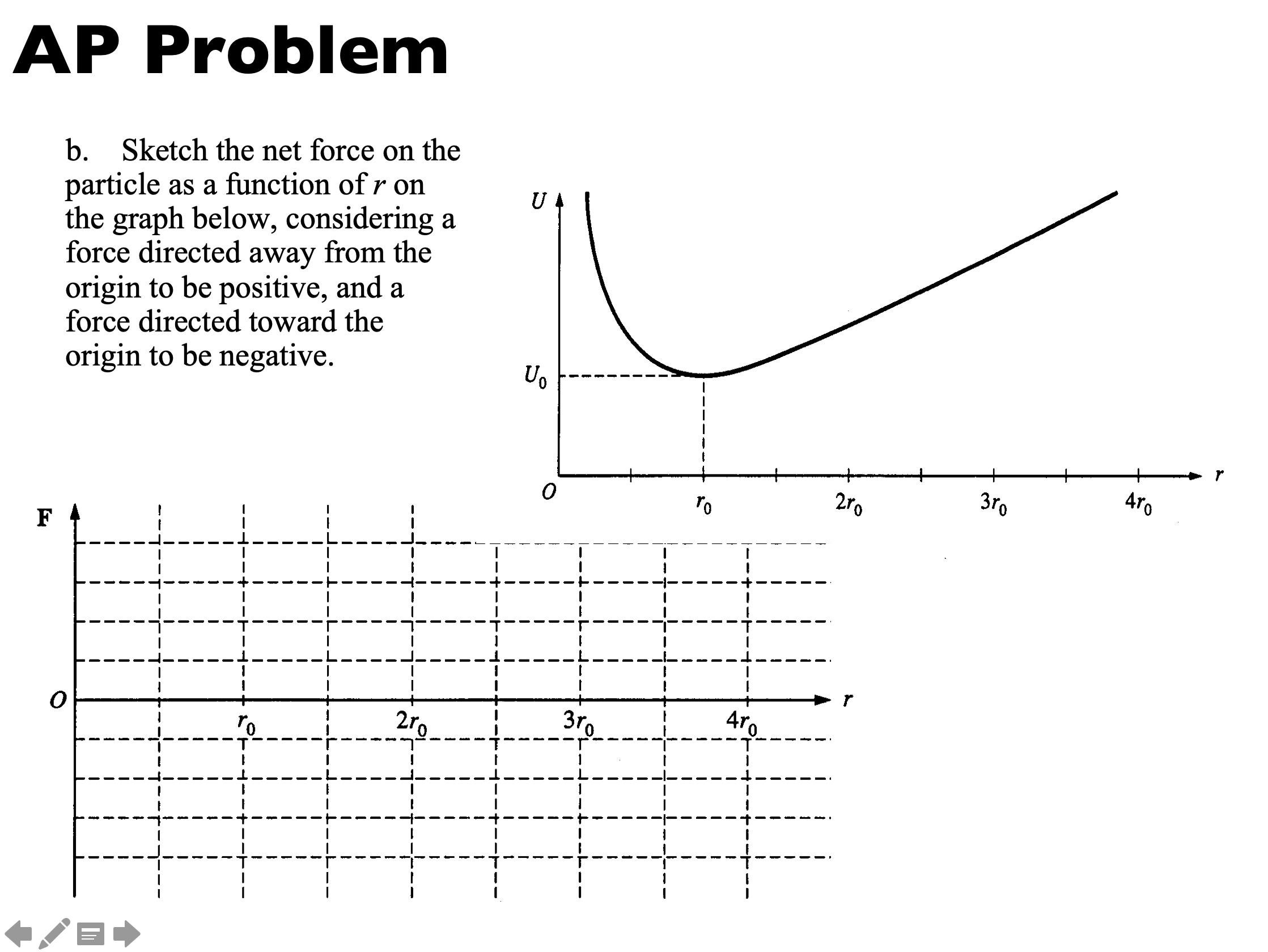
  1. concave up, crossing x-axis at r0, flat from 2r0 on at a negative-y value

Answers:

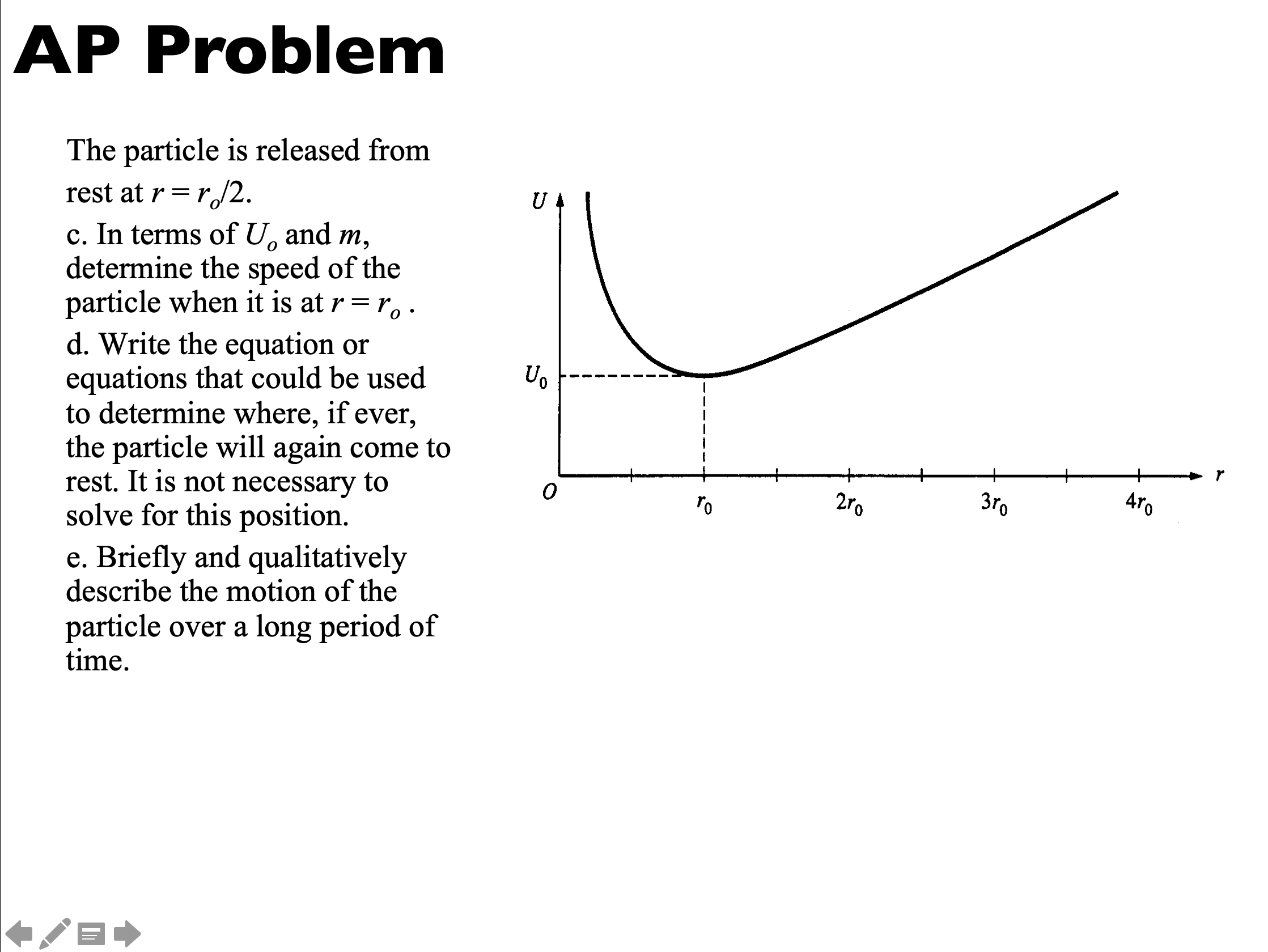
  1. Particle is released from rest, so total mechanical energy is U + K = all U at r0 / 2. That potential energy starts to be converted to kinetic. Use cons of mech energy to determine that v = √(U0/(2m))
  2. U(r1) = U(r0/2)
  3. Particle will oscillate, energy is not lost