
Chapter 6: Circular motion; more forces
6.0. Overview
We've had an introduction to Newton's Laws of Motion, and how we can use free-body diagrams with Fnet = ma to solve some interesting problems. In this section we'll continue that study.
Let's get started!
- Sliding Friction
- Centripetal force
- Horizontal circular motion
- Vertical circular motion
- Non-uniform circular motion
- Centrifugal force?
- Resistive forces
6.1. Friction
The subject of friction is where we finally get to expand our knowledge of physics to the point where we can finally solve some (more-or-less) real world problems.
Definition: Friction
Friction = a force that opposes the relative motion of a body
There are a number of different types of friction, including rolling friction, fluid friction (liquid or gas), sliding friction.
In this course we will primarily be concerned with sliding friction, the lateral friction that is present when two surfaces are in contact with each other and they are (possibly) sliding across each other.
We will also discuss fluid friction a little later on in the course.
6.1.1. Sliding Friction
When two surfaces are in contact with each other, a force that opposes their relative motion is called sliding friction.
The magnitude of this force of friction depends on two things:
- the nature of the two surfaces in contact with each other, as indicated by the "coefficient of friction" μ (the Greek letter "mu")
- how hard the two surfaces are being pushed together, as indicated by the normal force FN
6.1.2. Coefficient of Friction
The coefficient of friction μ is a number, experimentally determined, that describes how "sticky" two surfaces are when placed next to each other: the higher the coefficient of friction, the more sticky the two surfaces are, and thus, the more friction force there will be when they try to slide against each other.

Generally speaking, the coefficient of friction is a ratio that is calculated based on the measured force of friction versus the normal force measuring how much those two surfaces are being pushed together.
There are actually two different values for μ that we need to use, however, depending on the context of our situation.
If the two surfaces are not currently in motion relative to each other, the situation is described as static. The surfaces are not scraping against each other, and there is a force of static friction that prevents them from sliding. Examples of this include a car's wheels on the road as it is driving, a person's foot on the ground as she is walking, or a book resting on a tilted table (as long as the book is not sliding). In all of these cases, even when there is motion present, if the two surfaces are not sliding against each other, the friction is static, and the μ used to calculate that force is a μstatic.
If the two surfaces are sliding against each other—car wheels sliding on a wet road, a person slipping on an icy patch, or the book sliding down the table's surface if you tilt it far enough‐the situation is considered kinetic, and the force of friction is a kinetic one, with a corresponding μkinetic.
Although static and kinetic coefficients of friction are both concerned with surfaces that are attempting to slide against each other, they have different values. In a static situation the surfaces have not started moving against each other. Those "nooks and crannies" shown in the diagram above are locked into place, and have a greater ability to resist the sliding motion. Thus, the μstatic is relatively sticky compared with the μkinetic.
The μkinetic, on the other hand, describes situations when the surfaces are already in motion relative to each other. The nooks-and-crannies aren't locked into place the way they were before, and as long as the surfaces are moving, those rough edges are less likely to be able to grab hold of each other. There is still a force of friction, but it is less than the static force of friction that was in effect before.
So we can write the equations regarding sliding force of friction this way.
We'll come to understand these equations more as we use them to solve some problems.
MotoGP riders wear leather suits to protect themselves on occasions where they've fallen off their motorcycles.
6.1.2.1. The kinetic coefficient of friction
Let's look at some situations where there is sliding going on: kinetic force of friction problems.
A sliding box
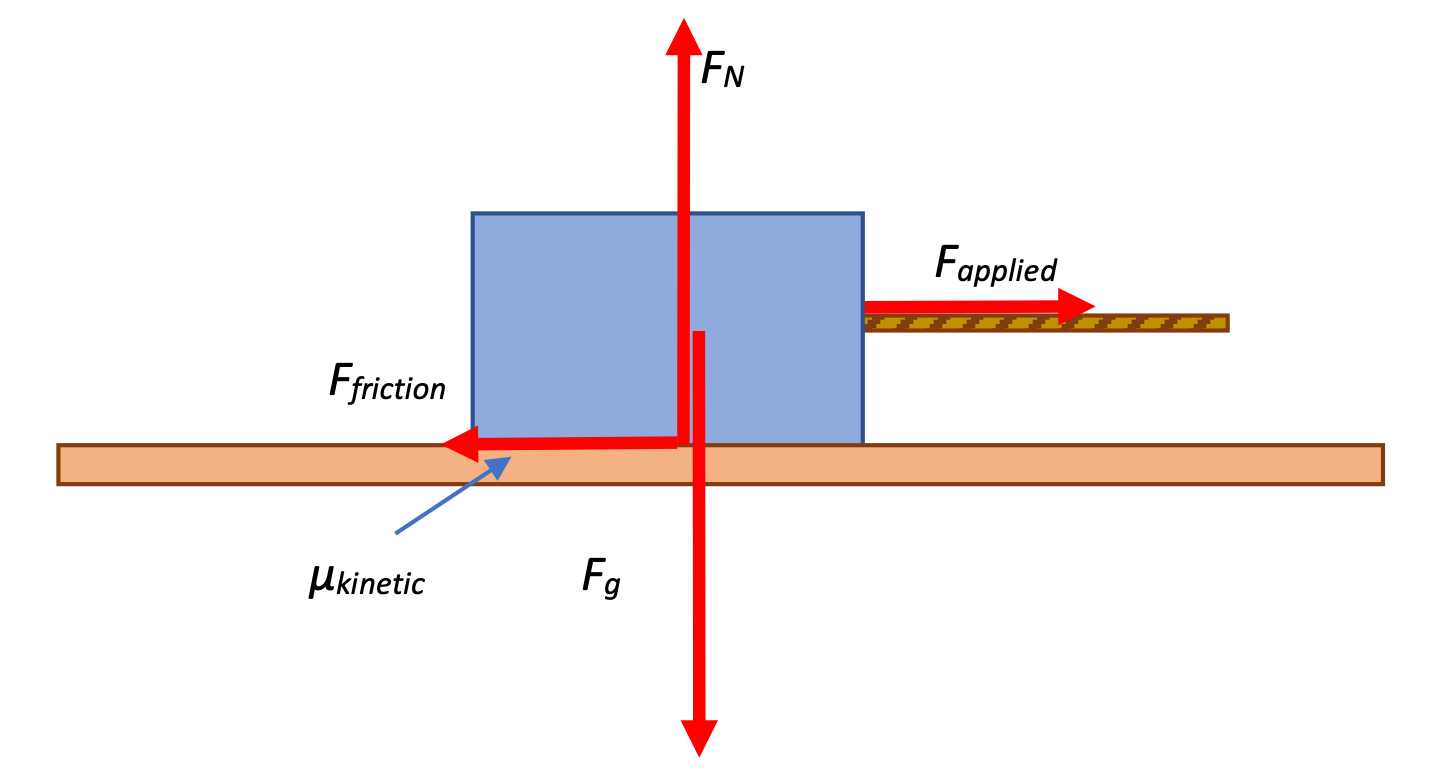
A wooden box with a mass of 5.0 kilograms is pulled across a table with a constant force of 20 Newtons, and it slides across the surface with a constant velocity. Is this a static or a kinetic situation? What is the acceleration of the box? What is the coefficient of friction between the box and the table?
This is a kinetic situation because the box is moving relative to the table.
The acceleration of the box is 0. We know this because the problem states that the box is traveling at constant velocity.
The coefficient of friction μk can be calculate based on:
How can we determine the Ffriction and the FNormal? Newton's Second Law of Motion, applied both vertically and horizontally.
Horizontally:
Vertically:
Finally, calculating μ:
Another sliding box
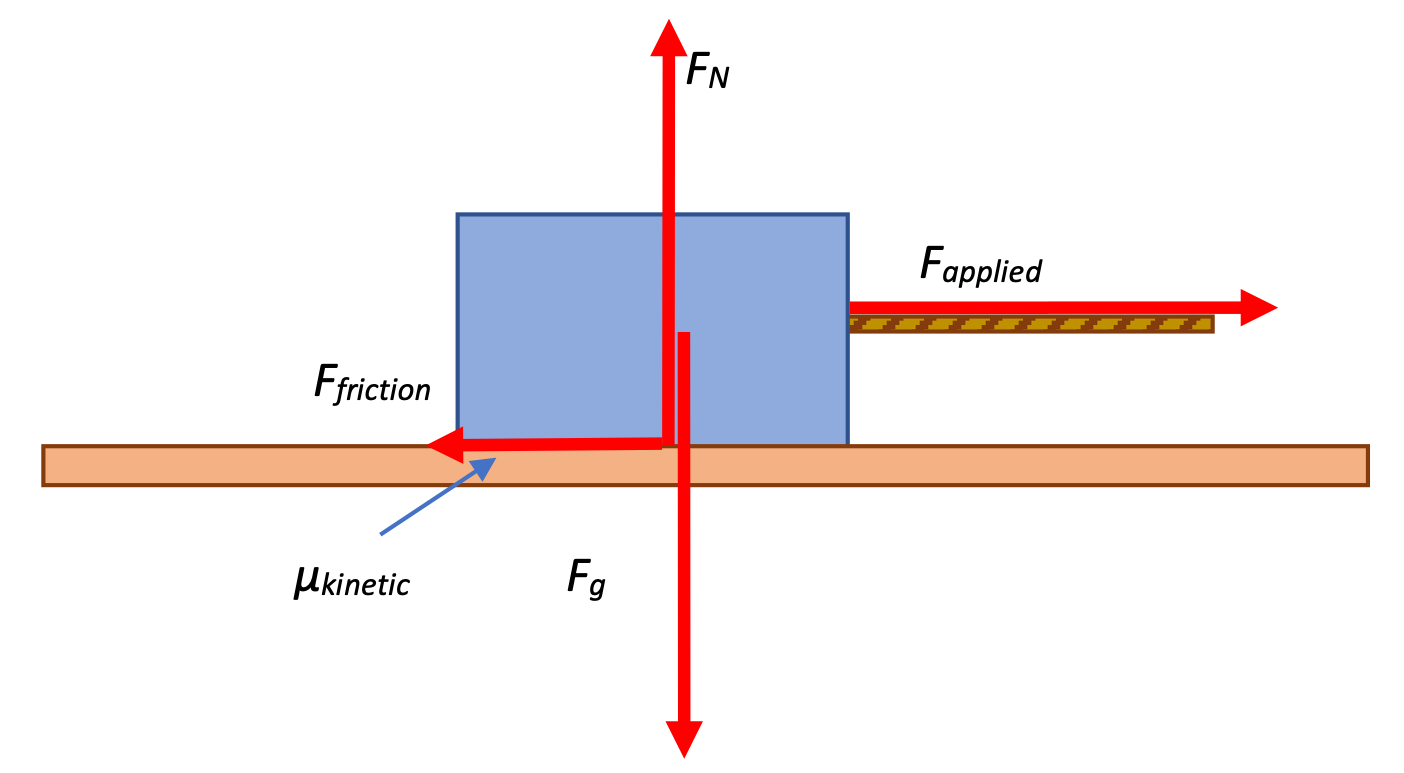
The same box as above is now pulled with a constant force of 40 Newtons. What is the force of friction acting on the box now? What is its acceleration?
The free-body diagram to the right looks almost exactly the same—the only difference is that the Fapplied vector is twice as long, due to it's magnitude being twice as large as in the first problem.
Note that the force of Friction hasn't changed—that depends only on the μ and the FNormal, and those two values haven't changed. We can calculate the acceleration of the box, then, using Fnet = ma, just as always:
Marquez slides to a stop
In the video above, MotoGP rider Marc Marquez falls off his bike and slides along the ground in the negative-x direction. Assume Marquez is traveling at 10 m/s when he goes down, and slides a total distance of 10 meters on the ground before he comes to a stop. Draw a free-body diagram of Marquez as he slides. What is the coefficient of friction between him and the ground?
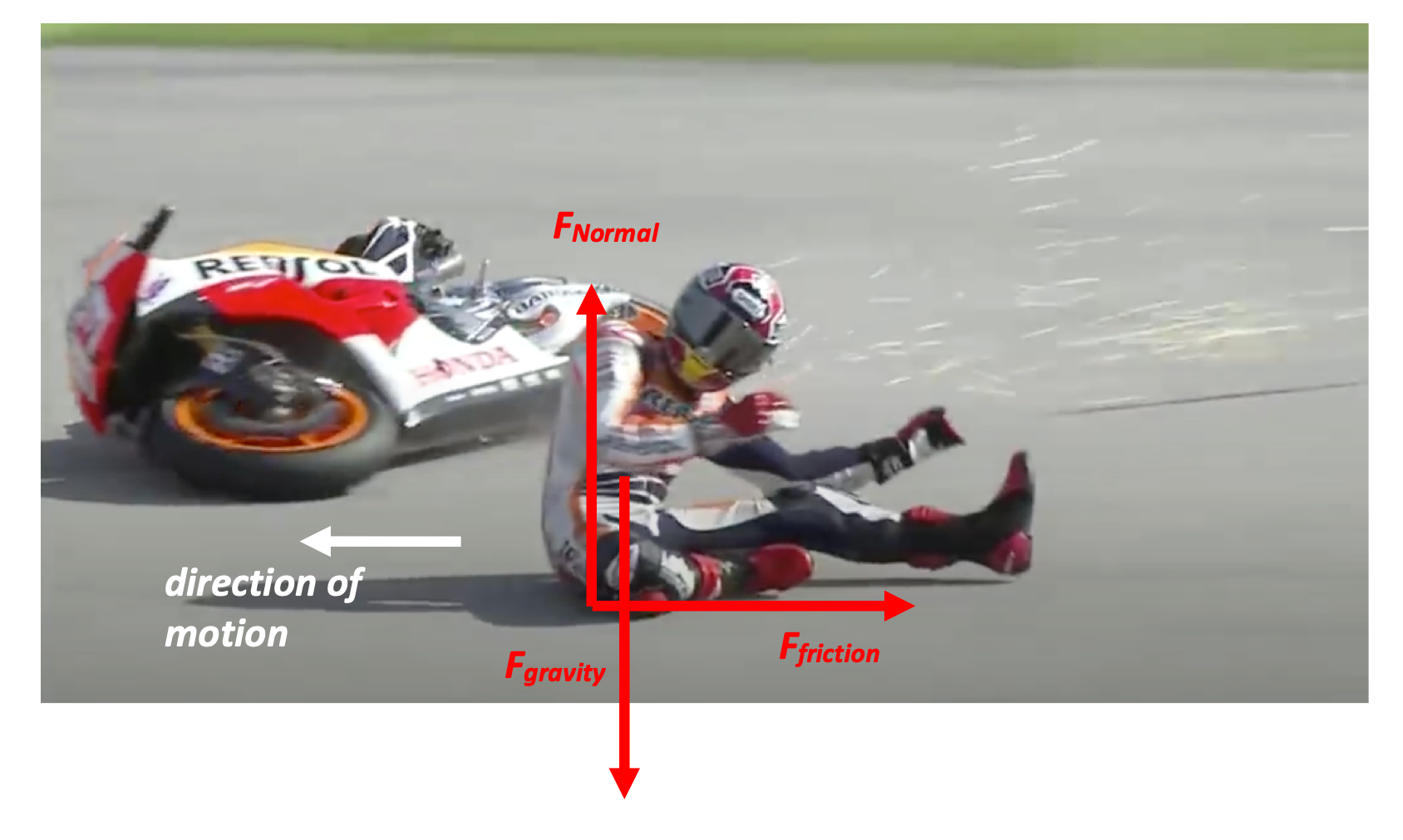
The free-body diagram here describes the forces acting on Marquez as he slides in the negative-x direction. To calculate the coefficient of friction, we need to know both the friction force and the normal force. Let's calculate the normal force first, knowing that there is no acceleration up or down:
And what's happening in the x-direction? There's an acceleration happening—a change in velocity—and we can use that to calculate the Ffriction:
Putting it all together:
6.1.2.2. The static coefficient of friction
The static coefficient of friction—used for situations where the two objects are not sliding relative to each other—requires some further explanation.
The static coefficient of friction can be used to calculate the maximum force of static friction between two surfaces, but that doesn't identify what the actual force of static friction is for any non-sliding situation.
Examine this first situation, where there is a "frictionful" (as opposed to "frictionless") boundary between the box and the surface it is sitting on. The only forces acting on the box are vertical. If there is no horizontal force to one side, there is no friction force either. The box is just sitting there.
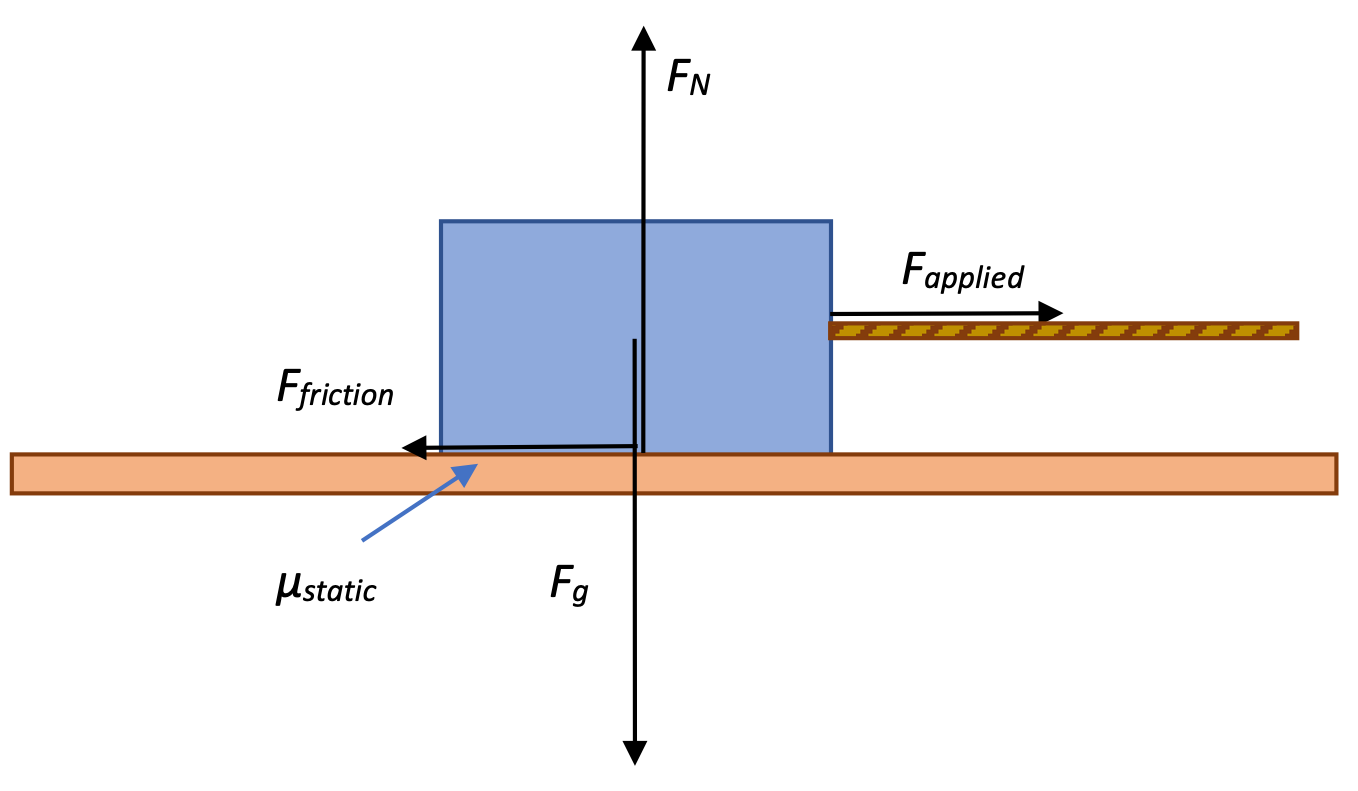
We'll now take a rope and apply a force to the right, just a small force. The box doesn't yet move, suggesting there is a force of static friction acting in the opposite direction to the applied force. There has to be a force in the opposite direction, because the Fnet in the horizontal direction is 0: the box isn't accelerating.
The Fapplied and the Fstatic are equal to each other.
What happens if we pull a little harder on the rope? Let's say the box still doesn't move. If the box isn't yet moving, there is no acceleration, and thus the horizontal forces must still be balanced. We've increased the Fapplied, and apparently the Fstatic has increased as well.
Pull a little harder and the box still doesn't move. The Fstatic has increased again!
This is getting a little frustrating; just how hard am I going to have to pull on this box to get it to start moving?
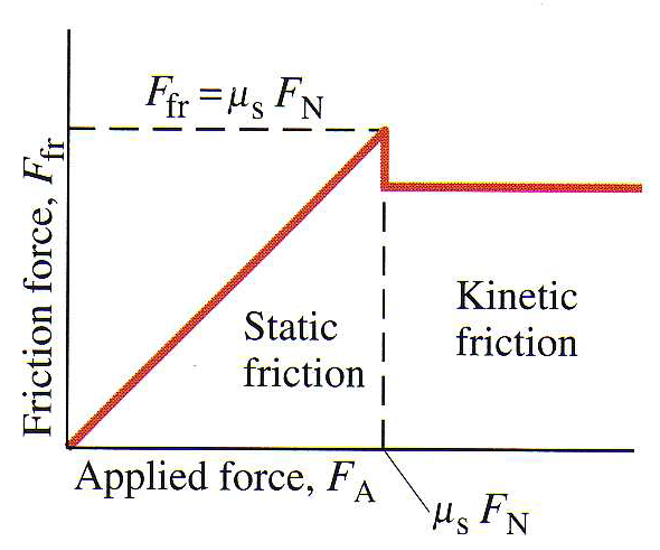
The maximum Fstatic, as described by the coefficient of friction, is the maximum force that the box can withstand before the surfaces break free and start to slide. Once we have a Fapplied > Fstatic, the box will start to move. (And at that point, we'll have to start analyzing it as a kinetic friction problem.)
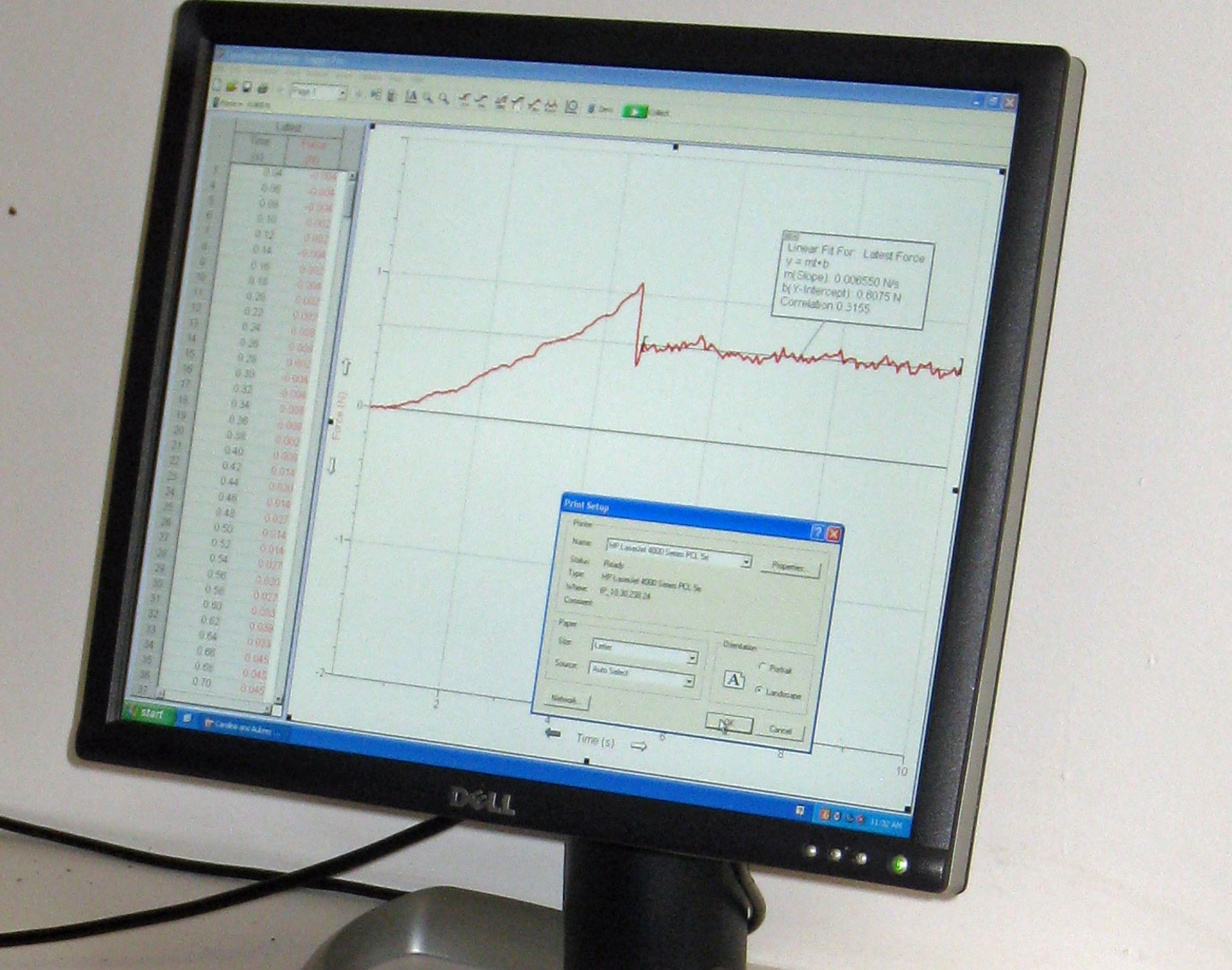
This changing static friction force is summarized in the graph here, on the left. As force applied increases, so does force of static friction, up to the point where the surfaces break free. The photo on the right shows experimental data collected that supports this explanation.
A sticky box
A wooden box with a mass of 2.7 kg rests on a wooden table. A cord is attached to one side of the box and pulled with a gradually increasing horizontal force. The box remains motionless on the table until it finally begins to accelerate when the Force applied to the cord is 20 N. What is the static coefficient of friction μstatic between the box and the table?
Based on the description of the situation, it looks like the maximum amount of static friction that the situation allows for is 20 N; after that, the box starts to move. So, the coefficient of static friction—the "stickiness" of the non-moving box on the table—is:
6.1.3. Table of coefficients of friction
Note that μs > μk ; once an object starts sliding (its maximum force of static friction being exceeded), the force of kinetic friction opposing that motion is less.
The relationship Ffriction = μFNormal is not a law; it's an empirical relationship.
| Surfaces | Coefficient of Static Friction (μs) | Coefficient of Kinetic Friction (μk) |
| Rubber on various surfaces | 1 to 4 | 1 |
| Rubber on dry concrete | 1 | 0.8 |
| Rubber on wet concrete | 0.7 | 0.5 |
| Steel on steel (unlubricated) | 0.7 | 0.6 |
| Wood on wood | 0.4 | 0.2 |
| Ice on ice | 0.1 | 0.03 |
| Human joints | 0.01 | 0.01 |
| Lubricated ball bearings | <0.01 | <0.01 |
6.1.4. Friction and inclined planes
Objects sliding down planes with a force of friction give us another opportunity to understand the interaction between Normal forces and friction.
Inclined plane with friction
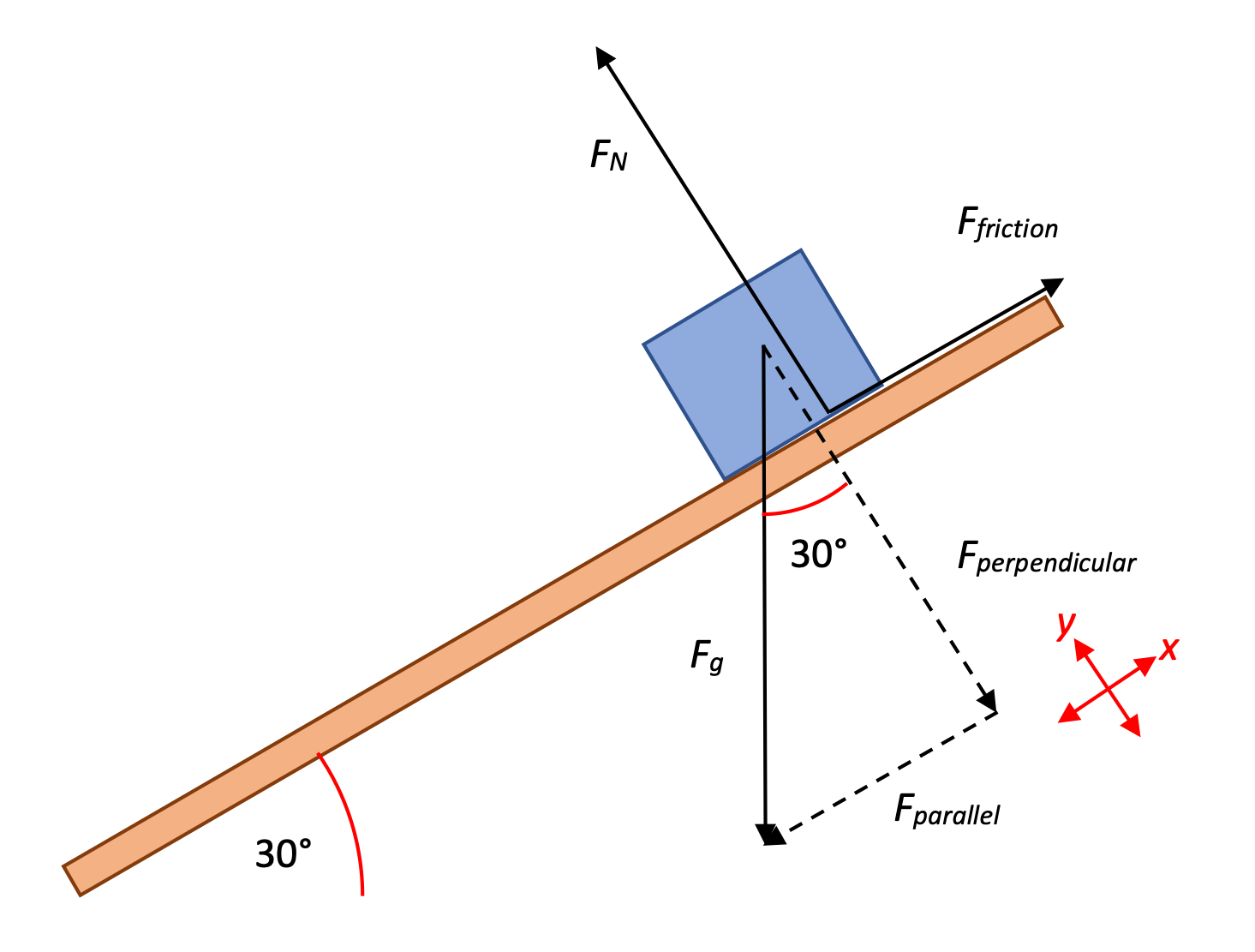
A skier, beginning from rest, descends a 30° slope where the kinetic coefficient of friction is 0.10. What is the freebody diagram for this situation? What is her acceleration? What is her speed after 6.0 s have passed?
The key to solving this problem, as with all of our problems in this unit, is:
- Drawing a correct free-body diagram, and
- Using Fnet = ma in each of the dimensions in our diagram to figure out what's happening.
Here I'm drawing the skier as a box, and I've included all the vectors acting on the skier/box: gravity, normal force (perpendicular to the surface), and force of friction (parallel to the surface and opposing her motion). Note that I've also tilted my axes for this analysis, because she's accelerating down the slope. This means I have to split my Force of gravity into Fparallel pulling the skier down the slope, and Fperpendicular holding her on to the slope.
With all the forces identified, we can use Fnet = ma in both the x and y directions to solve for her acceleration.
First the y direction:
Then the x direction:
Substitute and solve to get the acceleration down the slope:
And finally, what is the skier's velocity after 6.0 s have passed?
6.2. Centripetal force
An object moving along a circular path of radius r and constant speed v experiences a "center-seeking," or centripetal acceleration according to the equation:
But what force(s) actually cause the object to accelerate?
Centripetal force
Centripetal force is a way of describing any force that is acting to cause an object to accelerate centripetally. A force of tension, a force applied, a gravitational force, a Normal force, a friction force, can all act as a centripetal force, depending on the situation.
In analyzing circular motion problems, it is often convenient to use the variation on Newton's Second Law of Motion:
6.3. Horizontal circular motion
Let's begin our centripetal force analysis with an important example problem that will bring together a lot of the ideas we've been developing.
Car on a a Turn

A 1000 kg car on a flat road is traveling at 14 m/s on a curve of radius 50m.
- Draw a free-body diagram for the car.
- How much centripetal force will be necessary to keep the car on the road?
- If the μstatic for this road is 0.60, will the car make the turn?
- If the μstatic for the road is 0.20, will the car make the turn?
- What is the maximum speed the car can have and still make the turn with μ = 0.60?
- How high should we bank the turn to allow the car traveling at 14 m/s to stay on the track with no lateral friction from tires?
What are the forces acting on the car? Force of gravity pulling down on the car, and a Normal force from the road pushing upwards.
There is a force of friction, of course, that has to keep the car moving in a circle. If that force of friction weren't there, the car would go sliding off the road. Note that it's a static force of friction acting: although the car is moving, the tires are not sliding across the road—they are stuck there. (In this introductory problem, we'll avoid questions about rubber creep, drifting, etc.)
So, using the photo of the car to the right as a model, where the center of the curved road is to the right:

We know that it's the friction force that's acting centripetally, but in this question they're not asking anything specifically about friction. They just want to know, generally speaking, how much centripetal force is required to accelerate that car towards the middle of the circle?
Now we are being asked specifically about how much friction is involved. We're doing a static analysis, so one way to approach this is to ask the question, "What is the maximum static friction force this car has available to keep it on the road?" That "maximum static friction" is precisely what μstatic describes.
Because this maximum static force is much greater than the force we need to stay on the road, we can state that we will be able to make the turn.
Another strategy for solving this problem would be to calculate what the static coefficient of friction needs to be for the car to stay on the road:
We can see that the μstatic—the "stickiness" of the road—needs to be at least 0.40 for the car to make this turn. Because the problem stated that we have a μ that is greater (ie. "more sticky") than what we need, we see again that the car is able to negotiate the turn.
Based on our analysis above, we can see that the car needs μ = 0.40 to be able to negotiate the turn. If the μ drops to 0.20 due to water or oil on the road, the car will not be able to stick to the road. It will start to slide.
Instead of taking our known velocity and identifying a μ value, now we take a known μ and calculate for the velocity.

So we've seen that both the force of friction and a normal force can act centripetally to produce circular motion. Let's look at another example with a different force acting centripetally.
Mass on a string
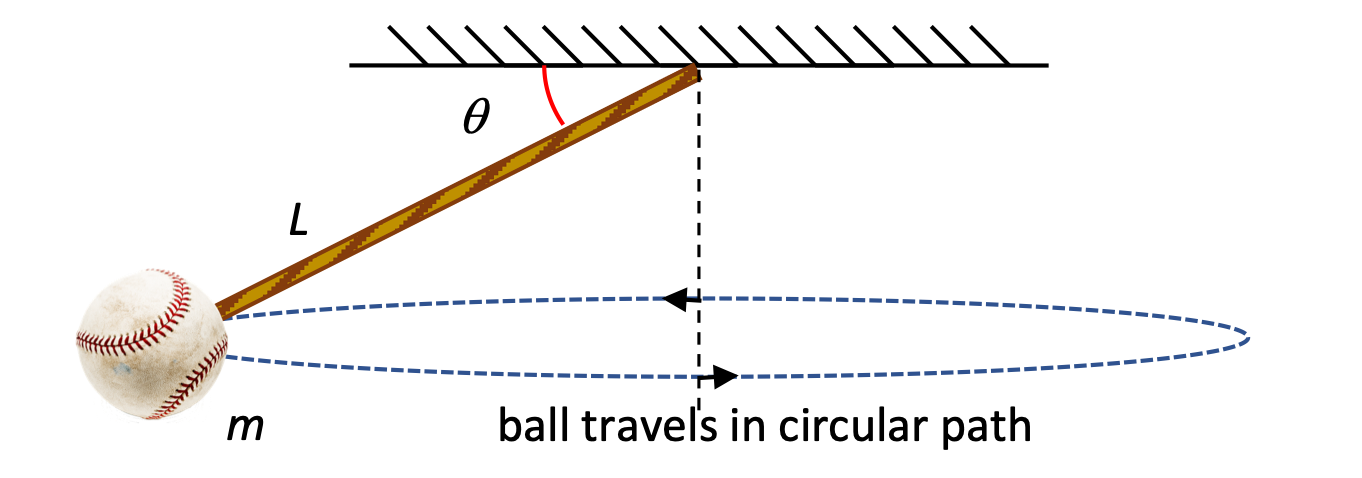
A baseball of mass m is suspended from a string of length L. As the ball is swung in a horizontal circle, the string makes an angle θ with the horizontal.
- Draw a free-body diagram of the situation, and determine whether you should tilt your reference axes.
- Find the speed of the body and the period (time) of one revolution in terms of L, θ, and fundamental constants (g, π, etc.)
- Calculate the tension in the string
"My Way"
Watch the video here, preferably with other students from class. As you watch the video, formulate answers to these questions:
- What acts as a centripetal force for the dancers in the performance?
- Are we watching static or kinetic friction forces in this piece? Explain how you know.
- At what locations on the platform is the centripetal acceleration the greatest?
- At what locations on the platform is the centripetal force the greatest?
- What do you think is the intended message of the choreographer?

6.4. Vertical circular motion
Objects traveling in vertical circles are treated exactly the same as objects traveling in horizontal circles: the sum of the forces acting on the mass add up to allow the object to accelerate centripetally, and thus, travel in a circle.
Ball swinging in a vertical circle
A 1.8-kg ball is swung in a vertical circle at the end of a 1.2-m long rope.
- What is the Tension in the rope as the ball swings past the bottom of the path at 5.0 m/s?
- What is the minimum velocity the ball can have at the top of its circular path?
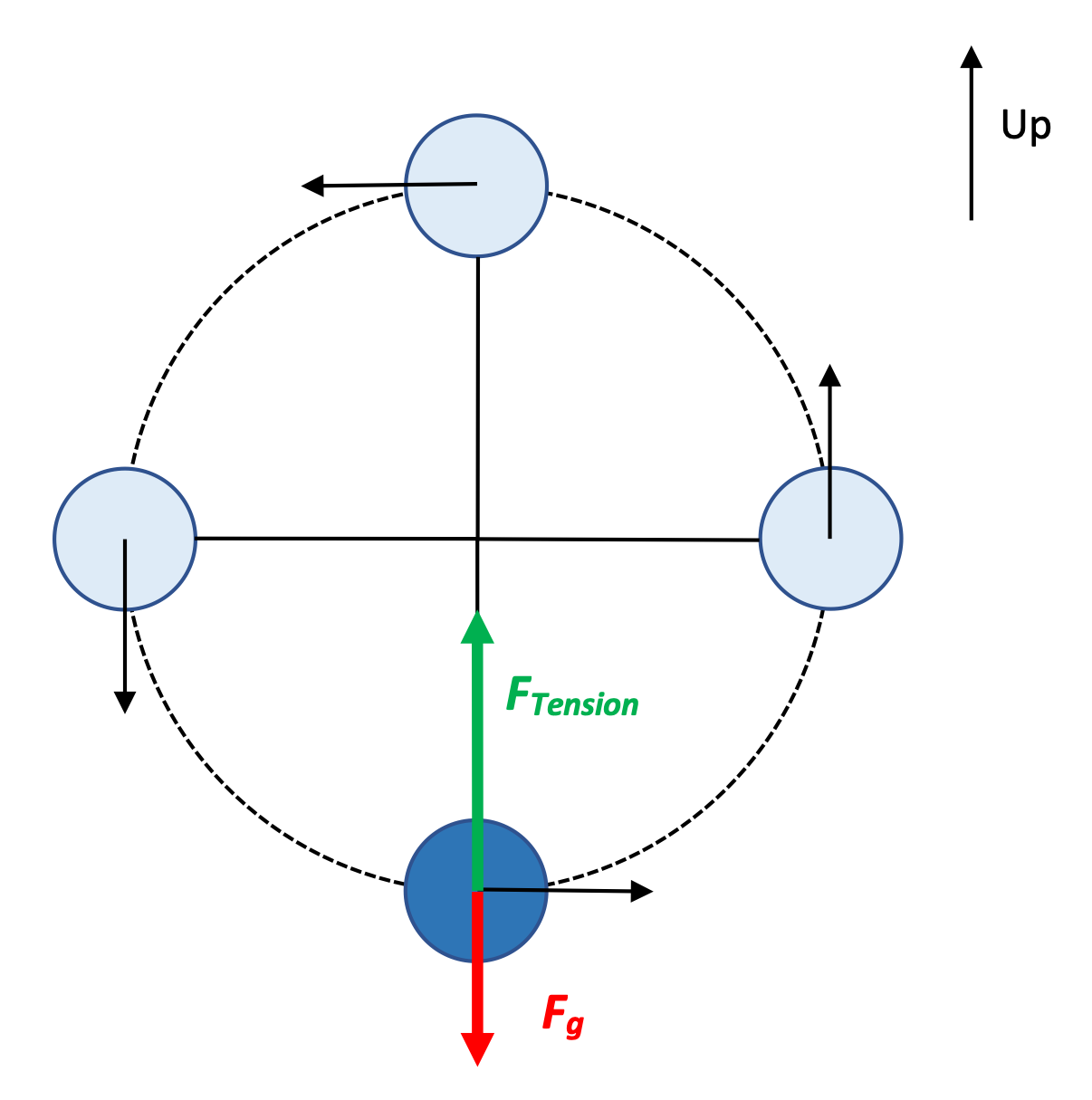
As always, we begin with a free-body diagram analyzing the situation. Notice that in this diagram the FTension vector is longer than the Fgravity, because we know there has to be a net force acting centripetally.
Then, Fnet = ma lets us analyze what's happening. Here, I'll consider the center of the circle to be in the positive direction.
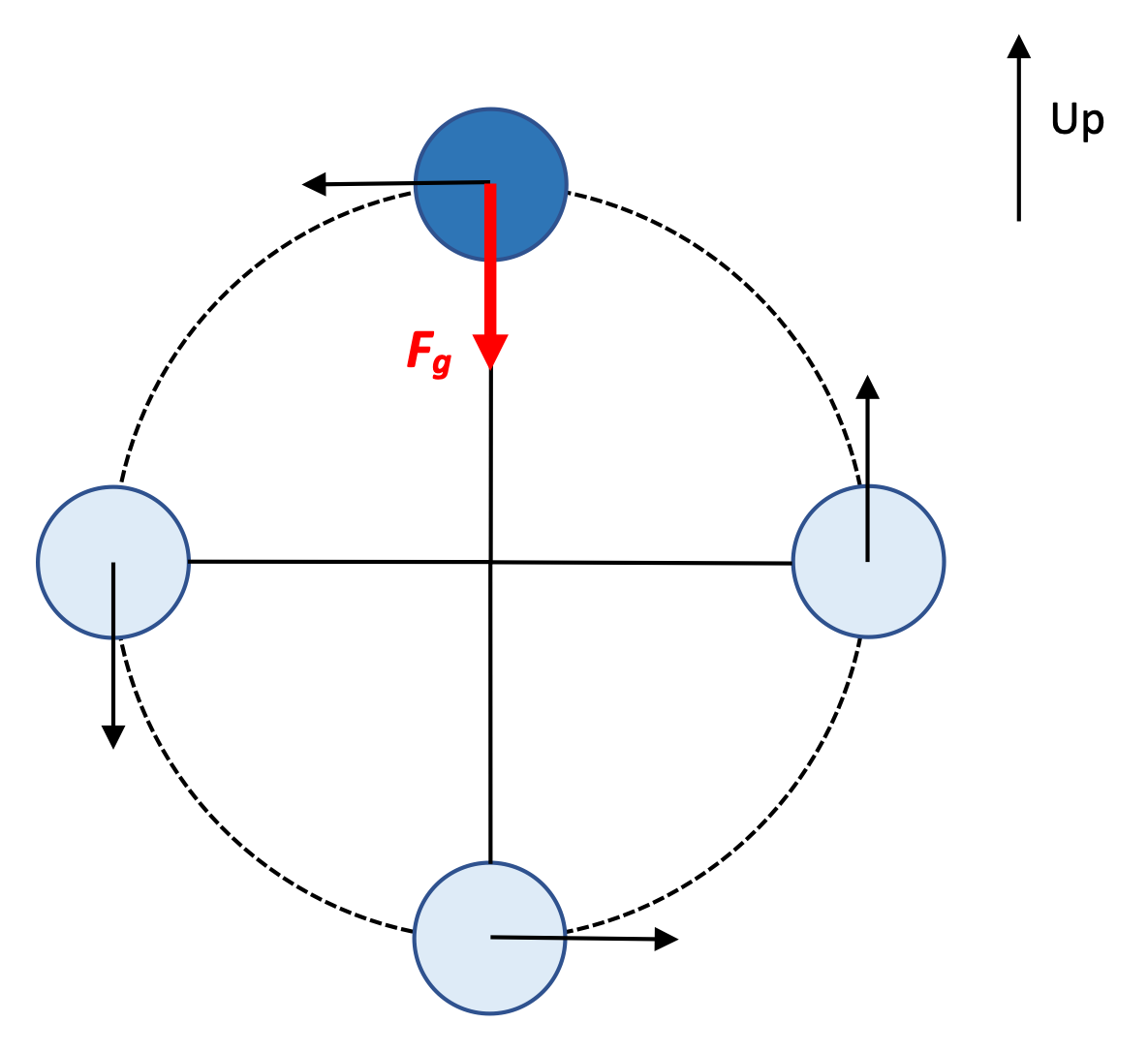
The free-body diagram here is a little less clear, perhaps. Gravity is still pulling down, of course. Is the Force of tension pulling down as well? For a ball traveling with a high velocity, we'll need a greater centripetal force, and so a force of tension would be needed in that case. That force, acting in the same direction as the force of gravity—down toward the center of the circle—would help provide a net centripetal force to keep this mass moving in a circle.
That's not what we've been asked for, though. We're trying to find the minimum speed the mass can have and still be traveling in a circle. That minimum speed corresponds with the minimum centripetal force, which is what we have when the force of gravity is the only force acting on the mass.
To solve for the minimum velocity, then:
Rollercoaster car in a vertical loop

A 100 kg rollercoaster car travels inverted through a vertically-oriented circular loop of radius 20 meters.
- At what velocity should the car travel through the top of the loop if the track is not to supply any force on the car?
- Describe the force supplied by the track if the car travels 5 m/s faster than this velocity.
- Describe the force supplied by the track if the car travels 5 m/s slower than this velocity.
6.5. Non-uniform circular motion
You may recall that earlier in this course we discussed the fact that an object moving along some curved path can be accelerating centripetally (as a result of its changing direction) and accelerating along the tangent to that curved path, as a result of its speeding up or slowing down. Those two aspects of the object's acceleration could be described in a "hat-theta" and "hat-r" unit vector format:
If we can describe the motion of a mass in terms of its tangential and radial accelerations, then it follows that those accelerations are due to tangential and radial forces.
6.5.1. Examples of non-uniform circular motion
One example of this kind of non-uniform circular motion involves a car speeding up (or slowing down) as it travels around a curved road. The force of static friction radially keeps the car on the road, and the force of static friction tangentially allows it to speed up or slow down.
The net force will be the vector sum of the radial and tangential friction forces.
Speeding up or slowing down?
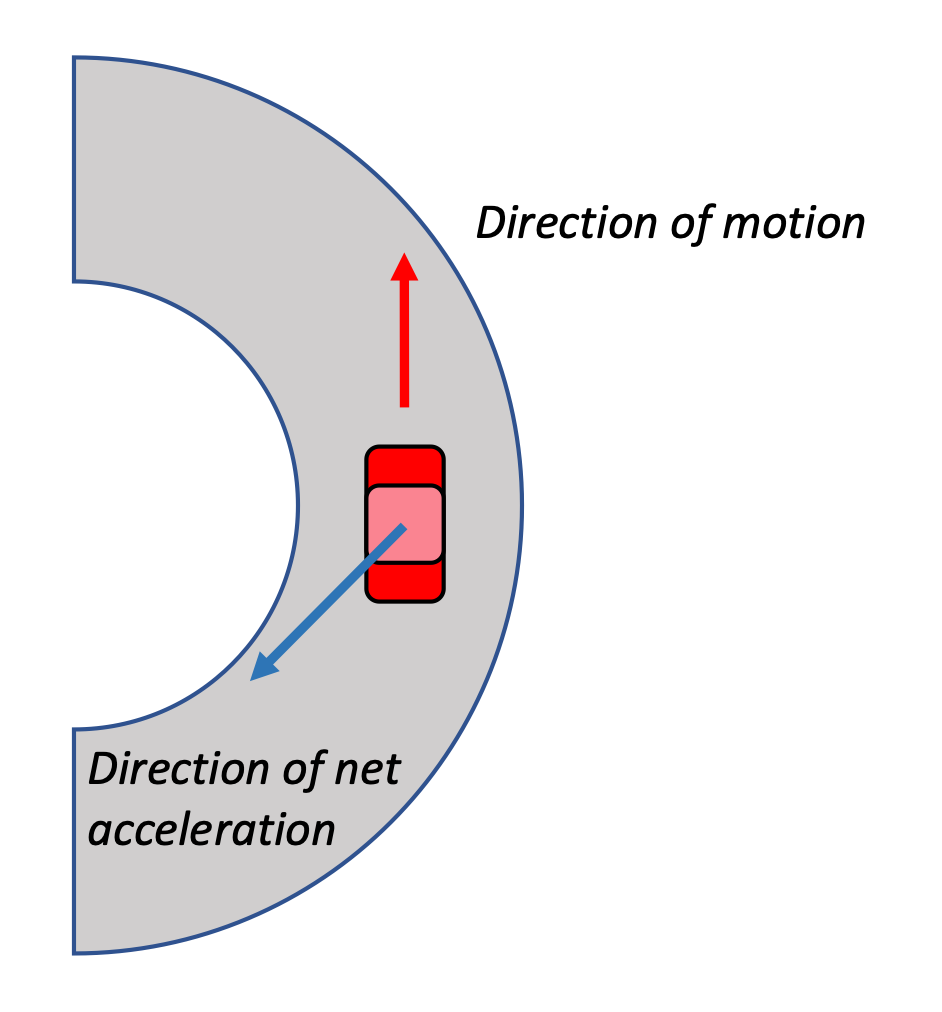
Is the car in this situation speeding up or slowing down? How do you know?
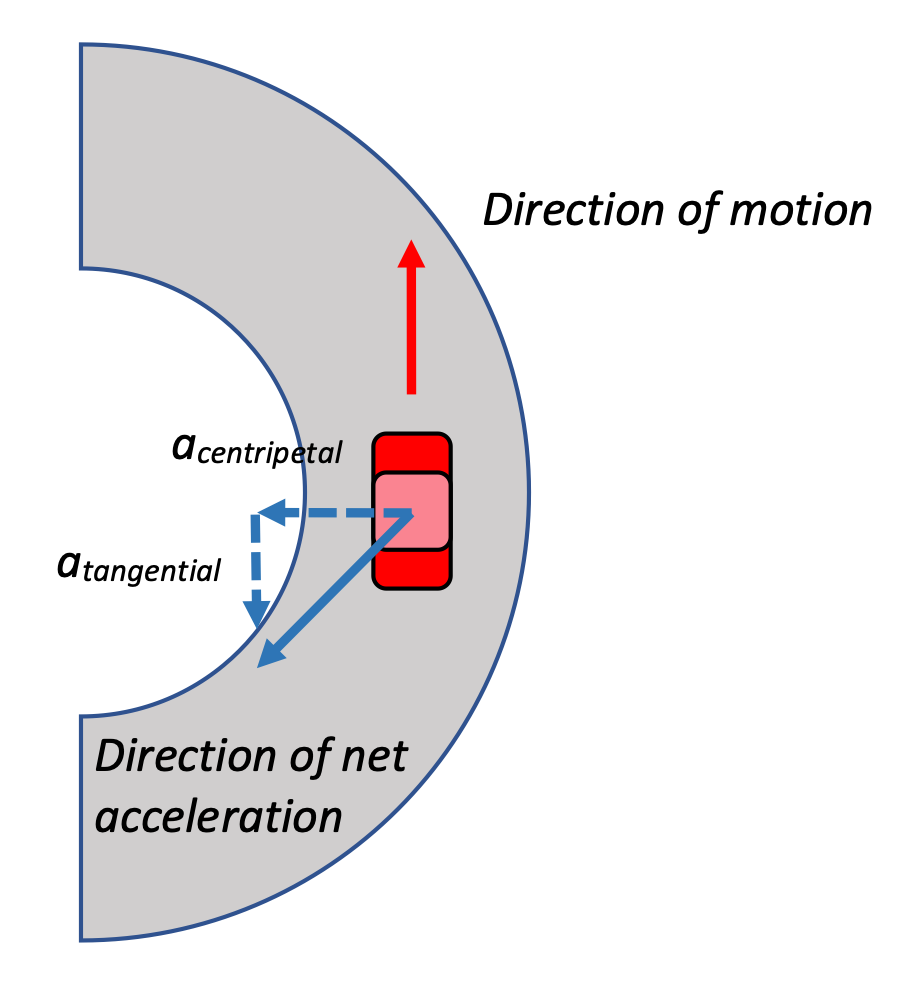
The net acceleration vector is made of two components, and we know one of them is the radial component that points toward the center of the curved path. That vector has to be able to add to the tangential vector to produce the net acceleration vector given. The only tangential vector that satisfies that condition is one that points in the opposite direction of the car's direction of motion. Therefore, the car must be slowing done on the curve.
Another example of non-uniform circular motion involves a pendulum swinging back and forth. Gravity acts on the mass of the pendulum, along with the tension of the supporting wire, string, or cord.
Analysis of a Pendulum
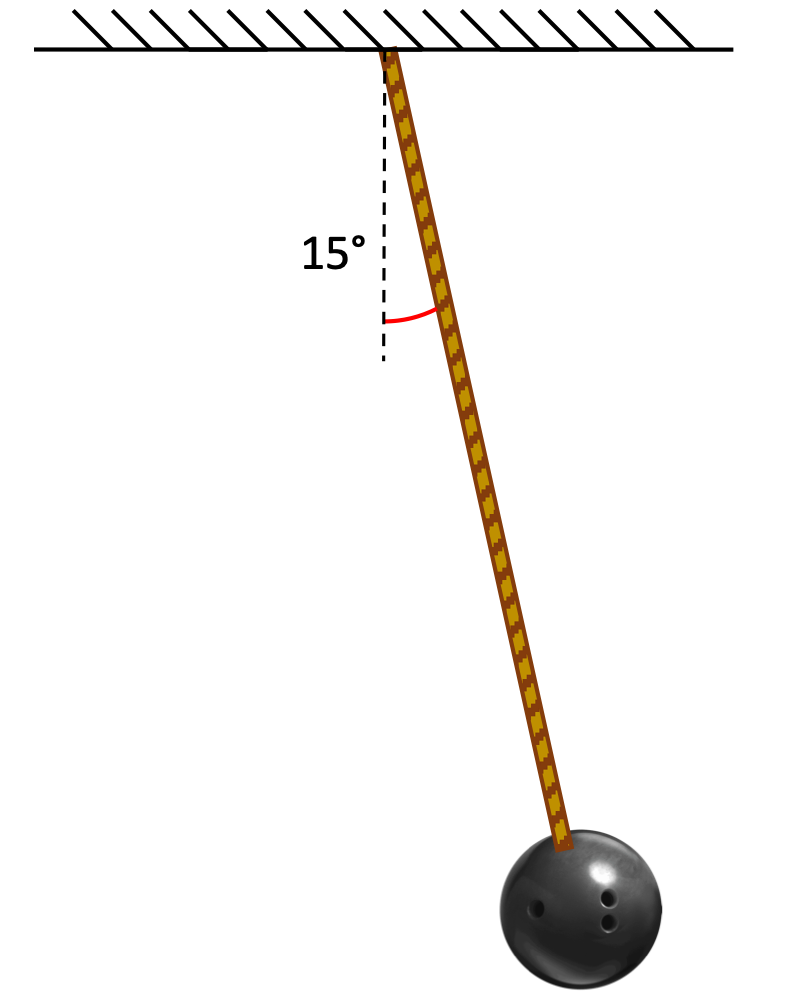
The bowling ball shown here is suspended by a long wire from the ceiling, pulled back a small angle, and released so that it oscillates back and forth. At a given moment in time, the wire of the pendulum makes a non-zero angle θ with the vertical, the ball has a velocity v, and is traveling in an arc with a radius r. Use these variables and the constant g in your solutions.
- Draw a free-body diagram of the pendulum when the wire makes a non-zero angle with the vertical. Will you tilt your axes for this analysis or not?
- Calculate the force of tension in the wire at this moment.
- Calculate the tangential acceleration of the ball at this moment.
- Calculate the radial acceleration of the ball at this moment.
- Express the net acceleration of the ball using unit vector notation.
- Express the net Force acting on the ball using unit vector notation.
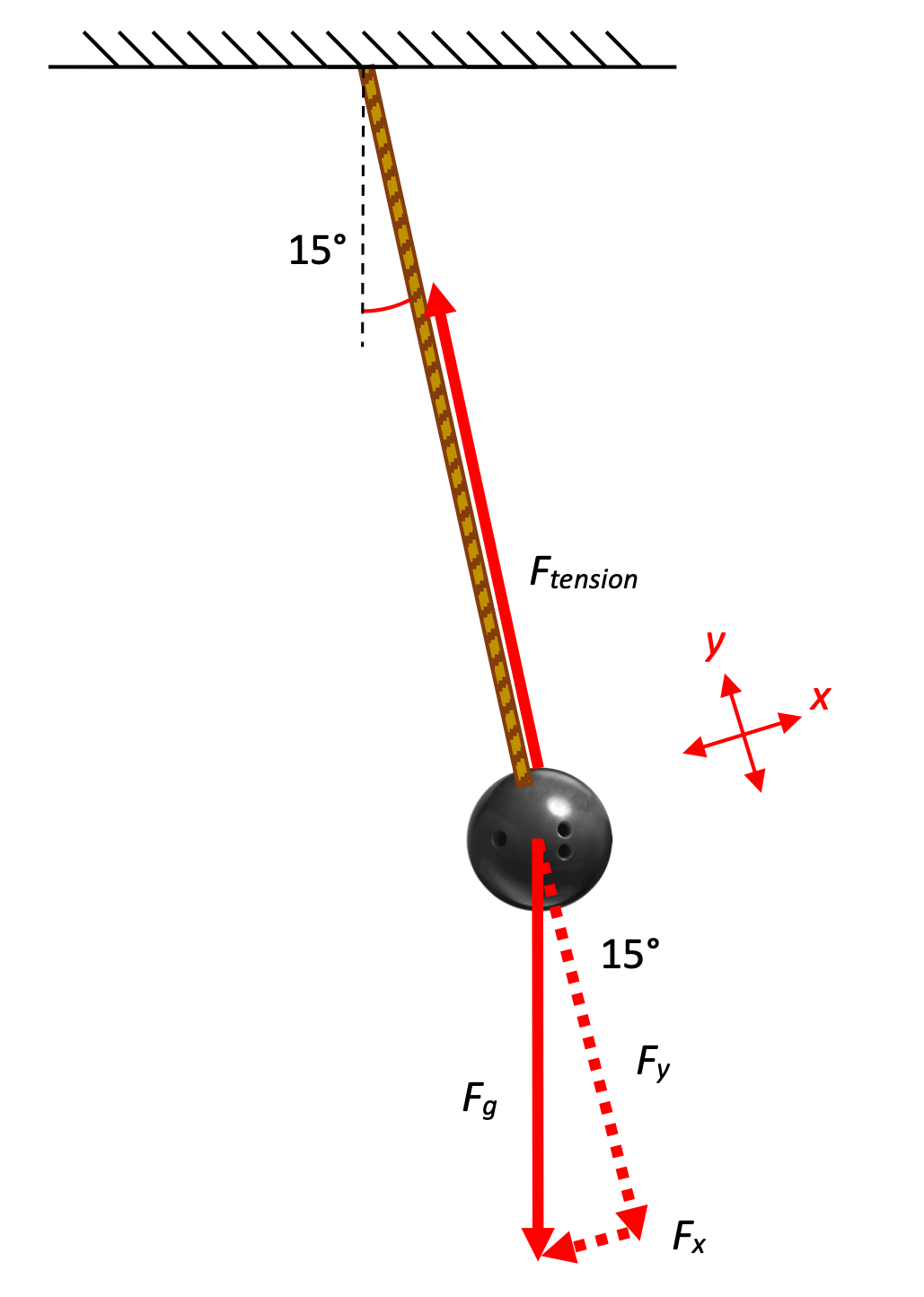
- The only two forces acting on the ball are the force due to gravity and the tension in the wire. Because the ball is accelerating radially (moving in a circle) and tangentially (as it speeds up and slows down), we're going to tilt the axes so they are aligned with those accelerations. This means that we have to take any vectors that are not aligned with radius or the tangent and break them up into radial and tangential components, which is what is shown in the diagram here.
- We can calculate the force of tension in the wire by using Fnet=ma in the radial direction:
- To calculate tangential acceleration, we'll need to know tangential force, because Fnet=ma in the tangential direction. There's only a single force acting in the tangential direction—the tangential component of the force of gravity—so this should be pretty straightforward:
- The radial acceleration of the bowling ball is also called the centripetal acceleration, and that's easy to calculate:
If we want to express that as a radial acceleration using unit vectors, remember that the unit "hat-r" points away from the center of the circle, and centripetal acceleration points toward the center, so we'd have to express it as a negative-hat-r:
- The net acceleration of the ball using unit-vector notation just uses the radial and tangential components that we've already calculated. The tangential acceleration of the ball at the location shown is clockwise, or negative-hat-theta, so:
- Net force is just mass time acceleration, and we've just calculated the acceleration. So,
6.6. Centrifugal force?

... doesn’t exist!
Centrifugal force is an "apparent" force that we mistakenly think pulls an object away from the center of the circle. There is no force pulling a rotating object outward!!!
In the case of the picture of the car shown here, the force of friction would ordinarily act as a centripetal force, pulling the car towards the center of the circular road and giving it a centripetal acceleration.
If the force of friction becomes too small—here it appears as if snow or ice have coated the road—the car slides off in a straight line motion as predicted by the principle of inertia: "an object in motion tends to continue in straight line motion, unless acted upon by a net force."
You can see the tracks of the car in the photo above, tracing its straight-line motion. There is no "centrifugal force" that pushes the car off to the side.
Take another example: If you're holding on to the string attached to the ball while it goes in a circle, it's true that your hand feels an outward pull: this is due to Newton's 3rd Law (your hand pulls on the ball to keep it moving in a circle, the ball pulls back on your hand).
If you let go of the string, the ball doesn't fly "outward" due to any supposed "centrifugal force." It flies in a straight line according to its direction of motion, based on the principle of inertia.
6.7. Resistive (Drag) forces
When a body is moving through a fluid substance (either a gas or a liquid), there is typically some resistance to the body's motion due to its interactions with the fluid.
More specifically, under these conditions we can describe a resistive force R (or Fdrag) that varies in some way according to the velocity of the mass through the fluid.
Depending on the circumstances, the resistive force may vary linearly with respect to velocity: R is proportional to v (R ∝ v) and as the velocity of the mass increases, so does the force of drag acting on it.
Or, resistive force may vary as the square of the velocity: R is proportional to v2: R ∝ v2
There are two common models that correspond to these two situations. One or the other will apply to a given set of conditions.
- Drag proportional to velocity:
- Drag proportional to velocity-squared:
6.7.1. Are we speeding up or slowing down?
There are one of two situations that we consider in this course. One is an object that begins to fall from rest, accelerating as it goes, up until the point at which it reaches terminal velocity. At that point the force of friction upwards equals the force of gravity down, and the falling object has reached its terminal velocity. It's still moving, of course, but it's no longer accelerating.
Another situation we might see is a mass that is moving with some initial velocity at time t = 0, and we start examining its velocity as it slows down as a result of the resistive force R.
There are other resistance scenarios that you might encounter, but these are two common ones.
6.7.2. Velocity as a function of time
Let's work our way through a typical analysis to see how we can use integrals to solve these problems.
A car slowing down due to air friction
A car is traveling to the right with an initial velocity vi when its engine dies. The car continues moving to the right, but a resistive force of friction R retards it's motion. R = -bv, where b is a positive constant.
- Derive an equation that describes the velocity of the car as a function of time.
- Calculate the velocity at time t = 10 s if the 1500 kg car has an initial velocity of vi = 25 m/s and b has a value of 20 kg/s.
- The car is moving to the right with a drag force acting to the left, opposite the direction of motion. Therefore:
We know that v is changing as a function of time, so let's express a as the time derivative of v. We can rearrange the equation so that the term with v in it is on the same side as the dv, and dt is on the other side.
In this expression, we're seeing the very small change in velocity that occurs over a very small period of time.
Finally, let's integrate both sides, the left with respect to v and the right with respect to t.
This is the relationship that describes v(t) for our car as it slows down. - Using the values given, we can determine that the velocity of the car at 10 s is 17.9 m/s.