Chapter 5: Newton's Laws
5.0. Overview
Newton's Laws is arguably the single most important topic in the study of Mechanics.
Let's get started!
- Some History
- Force, mass, and weight
- Newton's Three Laws of Motion
- Free-body Diagrams
- Solving Problems
- Inclined Planes
- Pulleys
5.1. Some History
5.1.1. Aristotle
Aristotle
Public domain image by Jastrow
The Greek philosopher & metaphysicist Aristotle (384-322 B.C.) based his analysis of falling bodies on pure logic: "Heavier objects fall faster in proportion to their weight." This belief was so logical that it persisted for almost 2000 years.
To be fair, Aristotle was right... a little. It turns out that heavier objects (in the atmosphere of the Earth) do accelerate more quickly (depending on their shape, and how fast they're going)... Aristotle was partly right, perhaps, but he didn't bother to test his ideas, and being able to test one's ideas is fundamental to science.
Aristotle also surmised that motion could be described as violent (a ball getting kicked, say) and natural (the ball rolling to a stop). The natural state of a body, according to Aristotle, is "at rest." That, too, turned out to be a little simplistic.
5.1.2. Galileo
Galileo
Public domain image by Dmitry_Rozhkov
Galileo (1564-1642) rebelled against blind acceptance of Aristotle's "logical" thinking, and encouraged repeatable experiments, earning him the "Father of Modern Science" title.
He also demonstrated, with a little logical thinking of his own, that Aristotle's ideas regarding "natural states of rest" were wrong.
5.1.3. Newton
Newton
Public domain image
Newton (1643-1727) continued Galileo's studies of motion. Newton wasn't known for publicizing his work, but in 1687, he published the Philosophiae Naturalis Principia Mathematica, which summarized his studies. This book was written in Latin, the language of scholars, and is considered by many to be the single greatest scientific book ever published.
Among other things, it included his analysis of motion, summarized in three laws.
Before we get to that, though, let's clarify the difference between three important concepts, all of them important to our understanding of Newton's Three Laws of Motion.
5.2. Force, mass, and Weight
These three important concepts are related in some subtle ways.
5.2.1. Force
A spring scale
Force = "a push or pull on an object". A force may not always cause motion, but it does cause deformation (change in shape), even if not always easily observable.
Forces have a magnitude and a direction, and thus, are vector quantities.
One of the most common ways of measuring force magnitude is with a spring scale.
The units of force are kg•m/s2, otherwise known as the Newton.
5.2.2. Mass
A 1-kilogram mass
Mass is one of the single most misunderstood concepts in chemistry and physics. It is not the same as "weight," although the two measurements are related.
Mass is a measure of the amount of inertia that a body has—it's a measure of how hard it is to change an object's motion. The more mass you have, the more inertia you have, and the more inertia you have, the harder it is to get you moving (if you're motionless), or to stop your motion (if you're moving).
Mass is measured in kilograms. Historically, the official standard of measurement for mass was a one-kilogram mass. It was made in 1879, and is stored in a special triple-bell jar, kept at atmospheric pressure in Sèvres, France. Anybody who wanted to find the real mass of an object has to go to France, and compare it with "the real thing," using a "balance."
Measuring mass with a spring scale
Question:
A spring scale is used to measure forces. Can you measure mass with a spring scale?
Answer:
Well... sort of. Sometimes.
We can use a spring scale to measure the mass of an object on earth, because a given mass has a given weight on the earth. This won't work if we're out in space, though—earth's gravity won't pull the object down on the spring scale. Clearly, the "stuff" in an object doesn't just disappear when we go into space, so an object can still have mass, but be weightless. (In space, where a spring scale is useless, we have other ways of measuring an object's mass.)
5.2.3. Weight
Weight is a measure of how strongly earth's gravity pulls on a mass. It is a measure of Force, and written as Fg, or sometimes as W. As with all forces, its SI units are the kg•m/s2 (Newton).
The weight of an object at the surface of the earth may be calculated as follows:
You may also see this equation written as
Using W to indicate the force of gravity, however, is discouraged. Current thinking in physics pedagogy is that writing forces with an F is good for beginning physics students, because it reminds us that Weight IS a force, the force acting on an object due to earth's gravity.
5.2.3.1. Some questions on Weight
Question 1
"I weigh 79.0 kilograms." Is this an acceptable statement? If true, is it true out in space as well?
No; mass ≠ weight, although in common usage, one may hear this.
You will have the same mass out in space. Mass is the same everywhere. 1.00kg at Earth's surface = 2.21 pounds.
Question 2
"I weigh 174 pounds." Is this an acceptable statement? Is this true out in space as well? What's the relationship between a pound and a kilogram?
Yes, this is an acceptable statement, although we use SI units for force, where 4.45 Newtons = 1.00 pounds. Also, weight = force of earth's gravity, which varies with distance from Earth.
Question 3
"I weigh 774 Newtons." Is this an acceptable statement? If true, is it true out in space as well? What is the relationship between a Newton and a kilogram?
Yes, this is acceptable, but weight varies with distance from Earth.
1.00 kg = 9.8 N (according to Fg=mg).
5.3. Newton's Three Laws of Motion
5.3.1. The First Law of Motion - Inertia
The Law of Inertia
"Every body continues its state of rest or uniform speed in a straight line, unless it is compelled to change that state by a net force acting on it."
This tendency to maintain one's state of motion (whether actually moving or at rest) is called inertia; for this reason, the Newton's First Law of Motion is commonly called "The Law of Inertia."
Which has more inertia?
A bowling ball is about the same size as a soccer ball. Which has more inertia?
Solution:
If you tried to run up and kick a bowling ball, you'd probably hurt yourself: it takes a lot more force to get a bowling ball moving than it does a soccer ball. The bowling ball has more inertia: it's harder to get it moving, and once it's moving, it's harder to stop it.
The bowling ball has more mass, and while mass can be thought of as a measure of how much inertia a body has, there are some interesting things to think about there.
5.3.2. The Third Law of Motion - Force Pairs
Newton's Third Law of Motion describes the relationship between the forces between two bodies that are interacting with each other
Newton's 3rd Law of Motion
"Whenever one object exerts a force on a second object, the second objects exerts a force (equal in magnitude, in the opposite direction) back on the first."
The Third Law is easy to state—you may have learned "for every action there is an equal and opposite reaction"—but it can be confusing.
Which force is greater?
When a baseball or softball player hits a ball, which is greater? The force of the bat on the ball? Or the force of the ball on the bat?
Solution:
The two forces—the ball on the bat and the bat on the ball—are equal to each other. In fact, they are the same force, a force of contact between the two objects, a result of the interactions between the atoms that make up those objects.
We typically think of the two forces separately, however. When we're focused on the ball, we think about all the forces acting on it: gravity, air resistance, the bat. And when we think about the bat, we consider the forces acting on it: the player's hands, gravity, the ball...
Identifying Force Pairs
One of the challenges in identifying force pairs is figuring out which forces are pairs of each other. You can tell force pairs by specifying both the thing that's being acted on and the thing that's acting on it. For example, there was the force "on the ball from the bat", and... the force "on the bat from the ball." The ball and the bat are interacting with each other.
If you're thinking about "the force on a soccer ball from earth's gravity" and "the force on a soccer ball from my foot," those are not force pairs. Both of those forces may be acting on the soccer ball, but they are not the "equal and opposite" forces described by Newton's Third Law.
Force Pairs
In this photograph, a rocket with an attached space shuttle is lifting off from the surface of the earth. There is a force of gravity acting on the rocket-shuttle, which is its weight.
True or False? The equal and opposite force of earth's gravity pulling down on the rocket is the force of the rocket's thrust pushing it up.
Solution:
False. There is a thrust force pushing up on the rocket, but that's not the "equal and opposite force" of gravity.
So what is the equal and opposite force? There has to be one, and it's easy to identify if you use the trick from the previous problem. The force pair of the earth's gravity pulling down on the rocket is... the rocket's gravity pulling up on the earth.
That sounds a little strange, but the force of gravitational attraction between the earth and the rocket is a single force acting on both of them. The earth pulls down on the rocket, and the rocket pulls up on the earth with the exact same magnitude of force.
5.3.3. The Second Law of Motion - Fnet = ma
Newton's Second Law of Motion describes what happens when a net (resultant) Force is applied to a mass. It describes what happens when you do try to kick a bowling ball. :-/
The second law, 
, can be used to solve a wide variety of problems.
Example 5.3.3.a. Accelerating the human body
Problem:
How much force is required to accelerate a 70.0-kg human from 0.00 m/s to 3.00 m/s in 5.00 s?
Solution:
Known values:
- v0 = 0 m/s
- vf = 3 m/s
- t= 5.00 s
- m=70.0kg
Unknown:
- a = ?
- F = ?
Formulae:
Solution:
Example 5.3.3.b. Accelerating a bowling ball
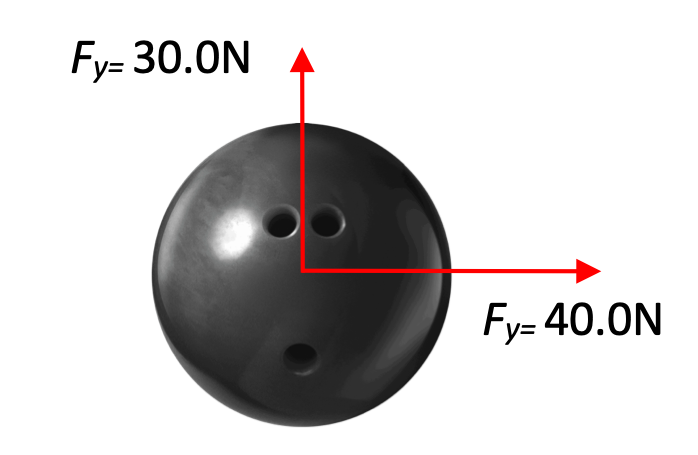
Problem:
A force of 30.0 Newtons is applied to a bowling ball in the 90° direction while a second force of 40.0 N is applied in the 0° direction. What is the net acceleration of the 10.0 kg bowling ball (magnitude and direction)?
Solution:
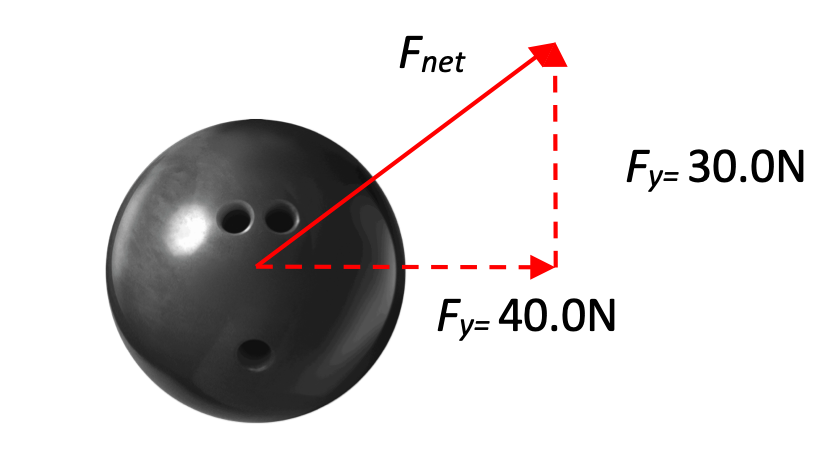
Known values:
- Fx = 40.0 N
- Fy = 30.0 N
- m = 10.0kg
Unknown:
- Fnet = ?
- a = ?
Formulae:
Solution:
5.4. Free-Body Diagrams
An apple sitting on a table
A free-body diagram is a sketch or drawing that identifies all of the vector forces (magnitude and direction) acting on a single object of interest, with the intention of analyzing what effect those forces have on the object.
5.4.1. Drawing force vectors
There are three rules for drawing force vectors. For each force that you identify as acting on an object:
- Draw an arrow so that it points in the direction of the force applied.
- Draw the arrow so that its base is located at the point where the force is applied.
- Draw the arrow with a length that represents the relative magnitude of the force.
5.4.2. The "Normal" force
It is often the case that there will be a surface that applies a force to an object—the surface of the table pushing up on the apple here, for example.
The general name for this type of force is the normal force, where the word "normal" means perpendicular to the plane of the surface.
In the case of the apple here, the FNormal from the table is directed upwards, but it's possible to have normal forces directed at an angle (if the surface is tilted), sideways (if a vertical surface is pushing against an object), or even downwards (if the surface is pushing down on the object).
We'll soon see examples of all of these.
An apple on a table
Draw a free-body diagram for the forces acting on an apple on a table.
Solution:
There are a number of forces acting in the diagram here—the force of Earth's gravity pulling down on the table, the force of the apple pushing down on the table, the force of the floor pushing up on the table, the force of air pressure acting all around both objects... but the only two forces of concern acting on the apple are the force of Earth's gravity down and the supporting force of the table upwards.
Those two forces are clearly indicated here, with an arrow pointing in the direction of the force, and the base of the arrow located at the point where that force is applied. The force of Earth's gravity acts on the center-of-mass of the apple, somewhere near the middle, and the table pushes up on the apple where the apple and table are in contact.
The lengths of the two arrows in this free-body diagram should reflect the relative size of the forces. We assume that the two forces are equal in magnitude, not because they are 3rd Law "force pairs"—they're not—but because the apple doesn't seem to be accelerating up or down. Without any further information, we assume it's sitting on the table, not accelerating, and therefore experiencing a net Force of 0. Hence, the two forces acting on it must be balanced.
5.5. Solving Force Problems
There are so many problems you can solve just by using Newton's Three Laws of Motion.
By judiciously applying our understanding of Newton’s Laws (especially the Second Law, Fnet = ma), we can analyze a lot of different situations.
In all of these situations, we’ll use the same problem-solving procedure:
- Identify & label forces acting on objects.
- Identify x- and y-axes on our diagram.
- Split angled vectors into x- and y-components.
- Apply Newton’s 2nd Law to x- and y- axes separately.
- Resolve x- and y- results into a single vector result with a magnitude and a direction.
Horizontal frictionless acceleration
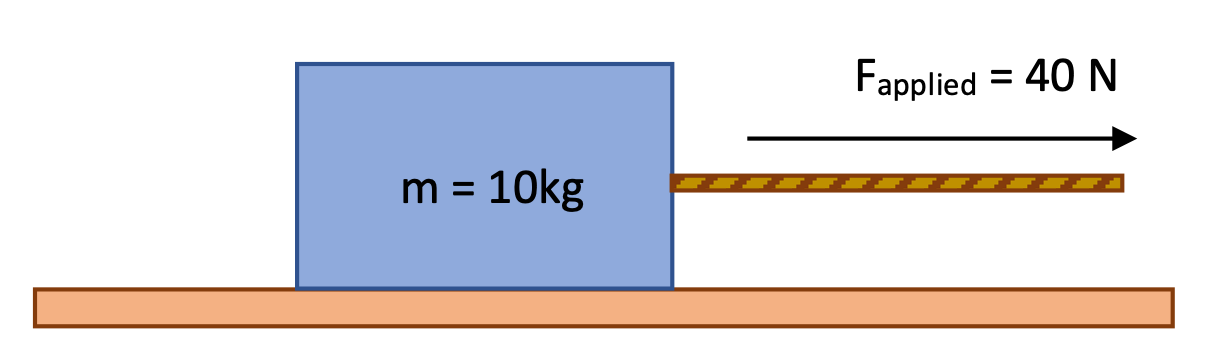
Determine the acceleration of this 10 kg box, initially resting on a frictionless table, and now being pulled by a rope with a force of 40 Newtons.
Solution:
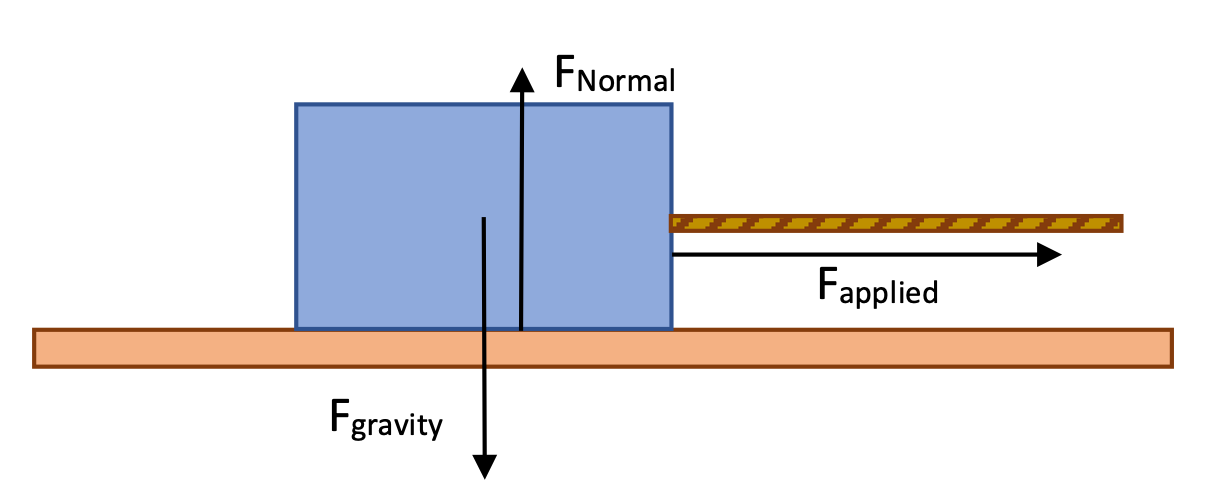
There are a lot of "frictionless" things when you're first learning physics, because dealing with friction is more challenging. We will be learning about friction very soon, but for now, imagine that a box on a frictionless surface has little wheels underneath such that the box is very easily able to start moving across the table.
Begin by drawing a free-body diagram. The box is only going to be accelerating to the right because that's the only net Force we have on it—the force of gravity and the normal force are going to balance each other out. How do we know that? Because there's nothing in this problem to suggest that the box is accelerating up or down. Therefore, if there's no acceleration, a = 0 and Fnet = 0.
That only leaves motion in the x-direction.
Horizontal frictionless acceleration?
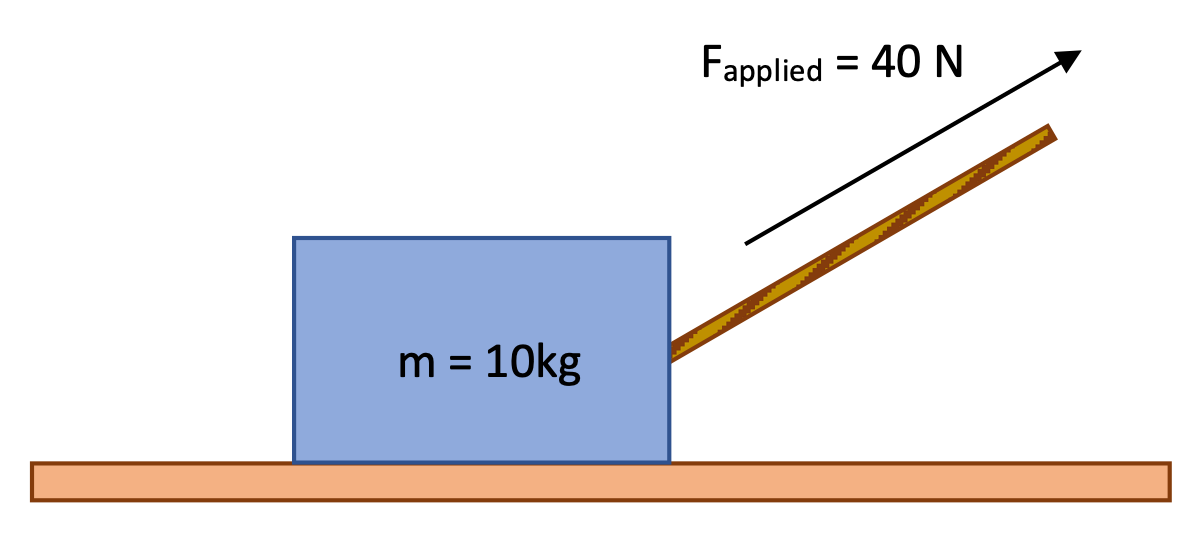
Determine the horizontal acceleration of this 10 kg box, initially resting on a frictionless table, being pulled by a rope with a force of 40 Newtons at an angle of 30° above the horizontal.
Solution:
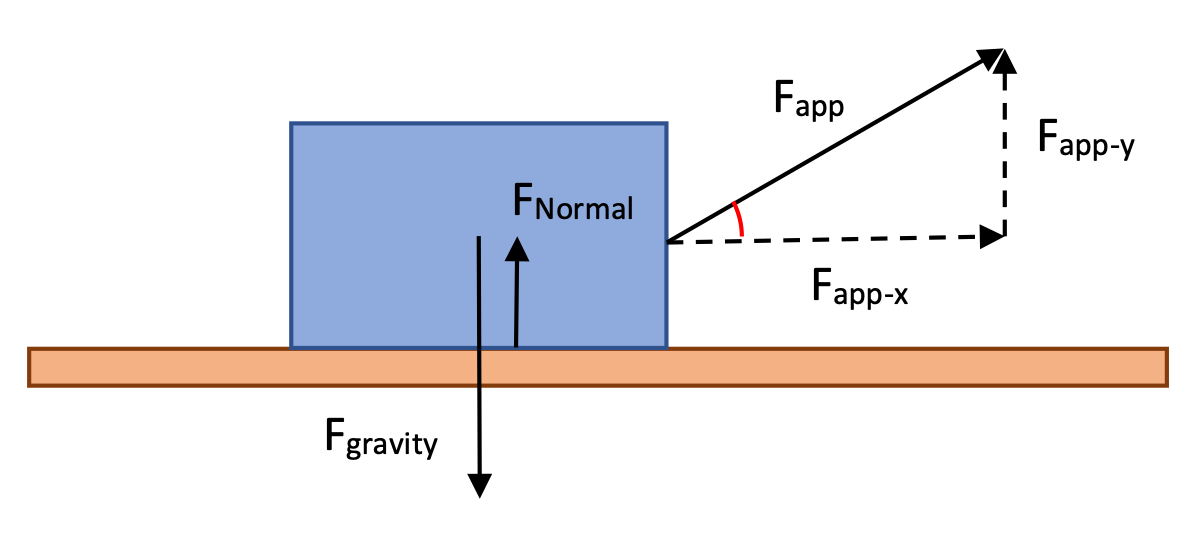
This problem is similar to the previous one: a rope is pulling on a box that is resting on a frictionless table. Here, though, the rope is pulling at an angle, so only some of the tension is pulling in the x-direction.
As always, to solve this problem you draw a free-body diagram indicating all the forces acting on the object of interest. Because we're being asked to consider the horizontal motion of the box, take the angled tension and draw the components of that force as dashed lies in the x- and y-direction.
Then use Fnet=ma to solve.
Find the Normal force
In the previous problem, what is the Normal force of the table that is pushing up on the box?
Solution:
We've already done the free-body diagram for this analysis in the problem above. Now we're considering what is happening in the vertical, y-direction. Again, we'll use Fnet=ma for our analysis.
I'll take the up direction to be positive, and put positive and negative values in for the FNormal (up), the Fgravity (down), and the y-component of the tension (up). I'm also going to assume that the box isn't accelerating upwards, so I'll set ay = 0. (It is possible, if we yank hard enough on the rope, to get enough upward force to lift the box up off the table. A quick check of our forces reveals that the upward force from the rope (20 N) is less than the weight of the box due to gravity pulling down (98 N), so the box isn't yanked up in this problem.)
Solving, then, in the y-direction:
A hanging mass
A mass of 2.5 kg hangs from a string attached to the ceiling. How much force does the string apply upwards to the box?
Solution:
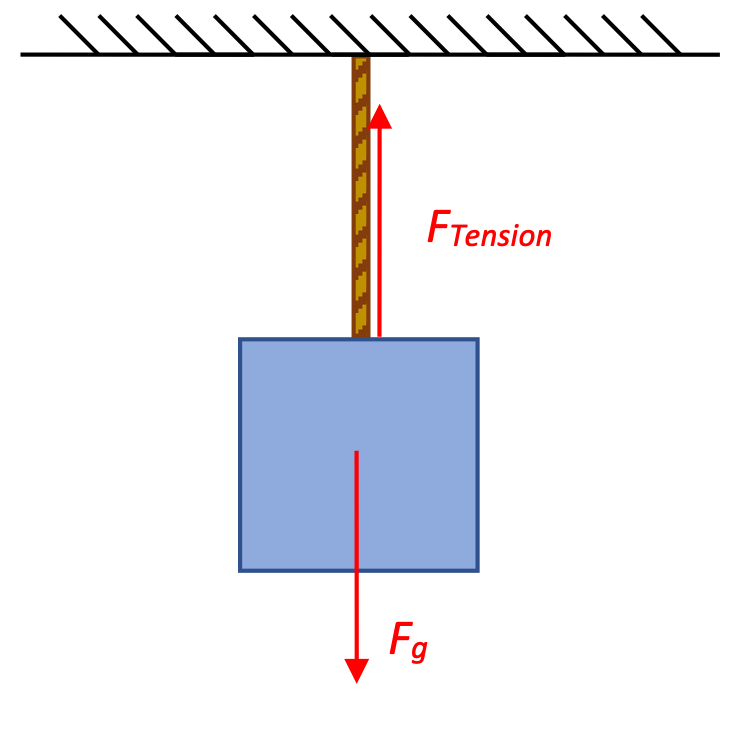
As always, let's start with a free-body diagram on the mass. It has a force of gravity pulling down on it, and the string pulling up on it. The mass isn't acceleration up or down, so the net force on it must be 0.
What is the tension in the cord?
A common question is, "What is the tension in the cord...?" For example, following up on the previous problem, "If the cord applies a force of 24.5 N upwards to the box, what is the tension in the cord?"
The potential source of confusion is that the cord is pulling up on the box with 24.5 Newtons, but the cord is also pulling down on the ceiling, with 24.5 Newtons. Do those two forces add together? Do they cancel each other out?
The answer is that the tension "in the cord" is that same value of 24.5 Newtons. If we were to place a very light spring scale ("light" so that it doesn't add its own weight to the problem) in the middle of the cord, it would indicate the force of tension as 24.5 Newtons. The entire cord could be made of little spring scales, and each of them would indicate 24.5 Newtons, measuring the force that is being transmitted throughout that connection.
In the same way that a force of gravity acts between two masses, the force of tension here acts between masses, and the cord is the means of transmitting that force.
Accelerating a hanging mass
A physics student holds on to a string that is attached to a 2.5 kg mass, and then starts pulling it upwards, accelerating it at 3.0 m/s2. How much force does the student have to apply through the string to get this acceleration?
Solution:
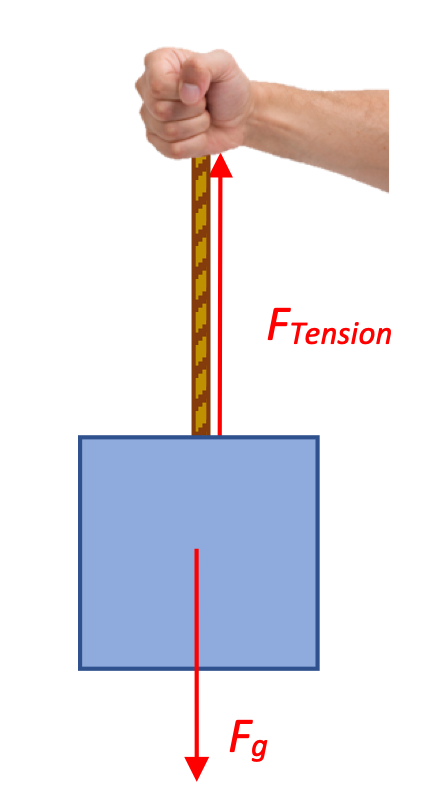
This is the same 2.5 kg (weight of 24.5 N) mass we had in the last problem. The student has to apply a force of 24.5 N via the cord just to hold the box steady.
If she actually wants to accelerate the box upwards she's going to have to exert an upwards force greater than 24.5 N. But how much exactly?
Notice in our free-body diagram that the upwards force of Tension vector is longer relative to the Force of gravity. This is good attention to detail, and shows that we expect to see the box accelerating upwards.
Two boxes accelerating
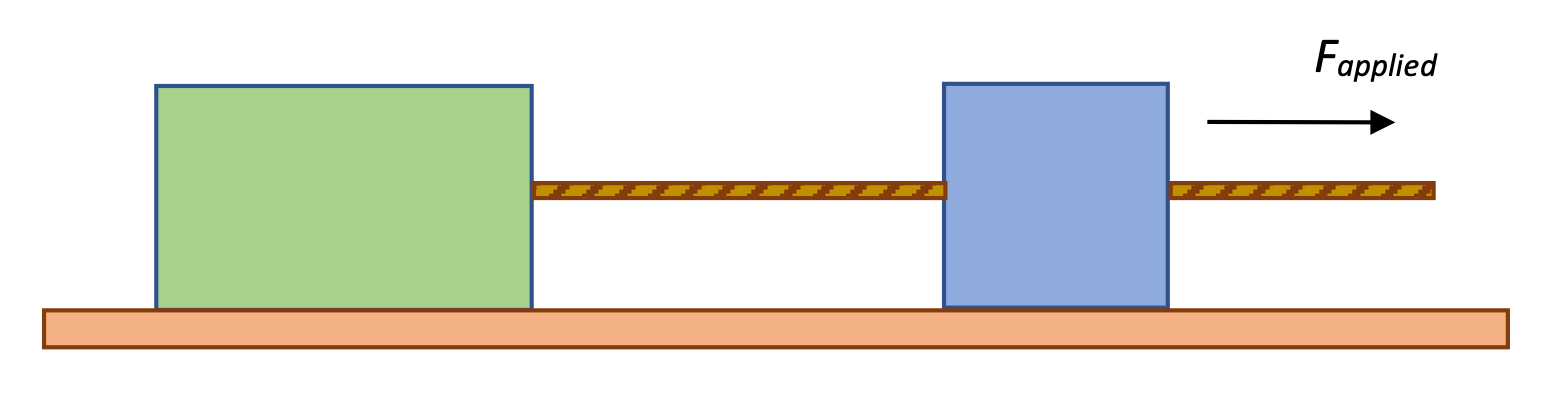
Two boxes resting on a table, one of mass m1 = 10kg and one of mass m2 = 20kg, are connected by a cord. A second cord is attached to m1 and a horizontal force of 60 Newtons applied via that cord. The blocks are able to slide with negligible friction along the table. Find the acceleration of each mass and the tension in each cord.
Solution:
There are a couple of ways to solve this problem. The first, and the one that you absolutely need to know how to do, is to consider the two masses separately. Draw a free-body diagram for each one...
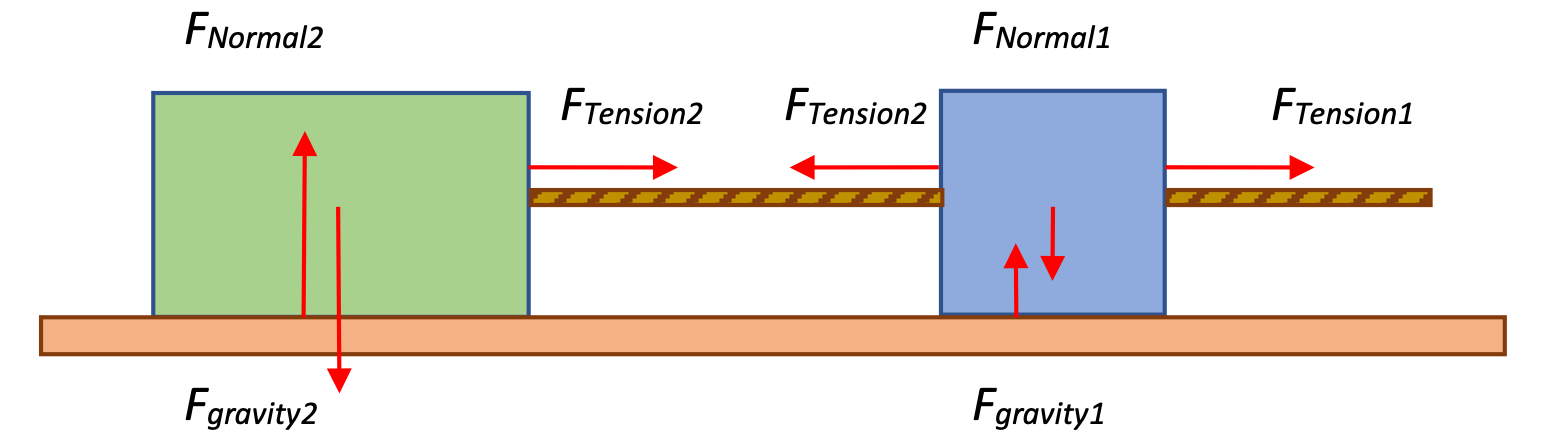
... and perform two separate Fnet = ma analyses for each one. Once you get the two equations, combine them to arrive at your answer.
Although our free-body diagrams include vertical vectors, we're only consider the horizontal motion here.
For the blue block on the right (m1), note that there are two tensions, the one force-applied pulling to the right and the tension from the cord attached to it on the left. We can guess that the force applied on the right is greater than the force on the left—otherwise, the block wouldn't be able to accelerate.
And for the green block on the left (m2):
Note the force pairs for the tension between the two blocks. That single force of tension, transmitted by the cord, pulls back to the left on block m1 and pull forward to the right on block m2. The magnitude of that force is the same, although the direction is different for each of those masses. We account for that in our equations by putting a + or a - to indicate the direction along the x-axis.
Also, the blocks have the same acceleration. Once m1 begins to move, m2 is dragged along with it. Thus, the acceleration a in this problem is the same magnitude and direction for both of them.
Combining those equations, then, to get the acceleration:
And substituting back in to get the tension in the second rope:
Did you notice the net force on m1 is 60-40 = 20 N, while the net force on m2 is 40 N, or twice as much? That makes sense, given that m2 has twice as much mass. It needs twice as much Force to give that larger mass the same acceleration.
Two boxes accelerating (for cheaters)
I'm only kidding about the cheating part. Although the problem-solving strategy described above is the best for when you want to be careful about making sure you understand every aspect of a problem, there is a shortcut you can use to solve the problem more quickly.
Solution:
Because the two masses are accelerating at the same rate, we can consider their two masses to be a single mass of 10kg + 20kg = 30kg. The net force of 60 N applied to the total mass of 30kg allows us to quickly calculate the acceleration:
What about the tension in the second cord? We can consider that tension to be "internal" to the system, with the two forces (equal in magnitude, opposite in direction) cancelling each other out. If we need to find out what's happening with that cord, we can again consider the masses separately, and perform an individual free-body analysis on each one of them.
In the meantime, if all you need to find is the acceleration of the system, you can easily apply this simplified approach.
5.6. Inclined Planes
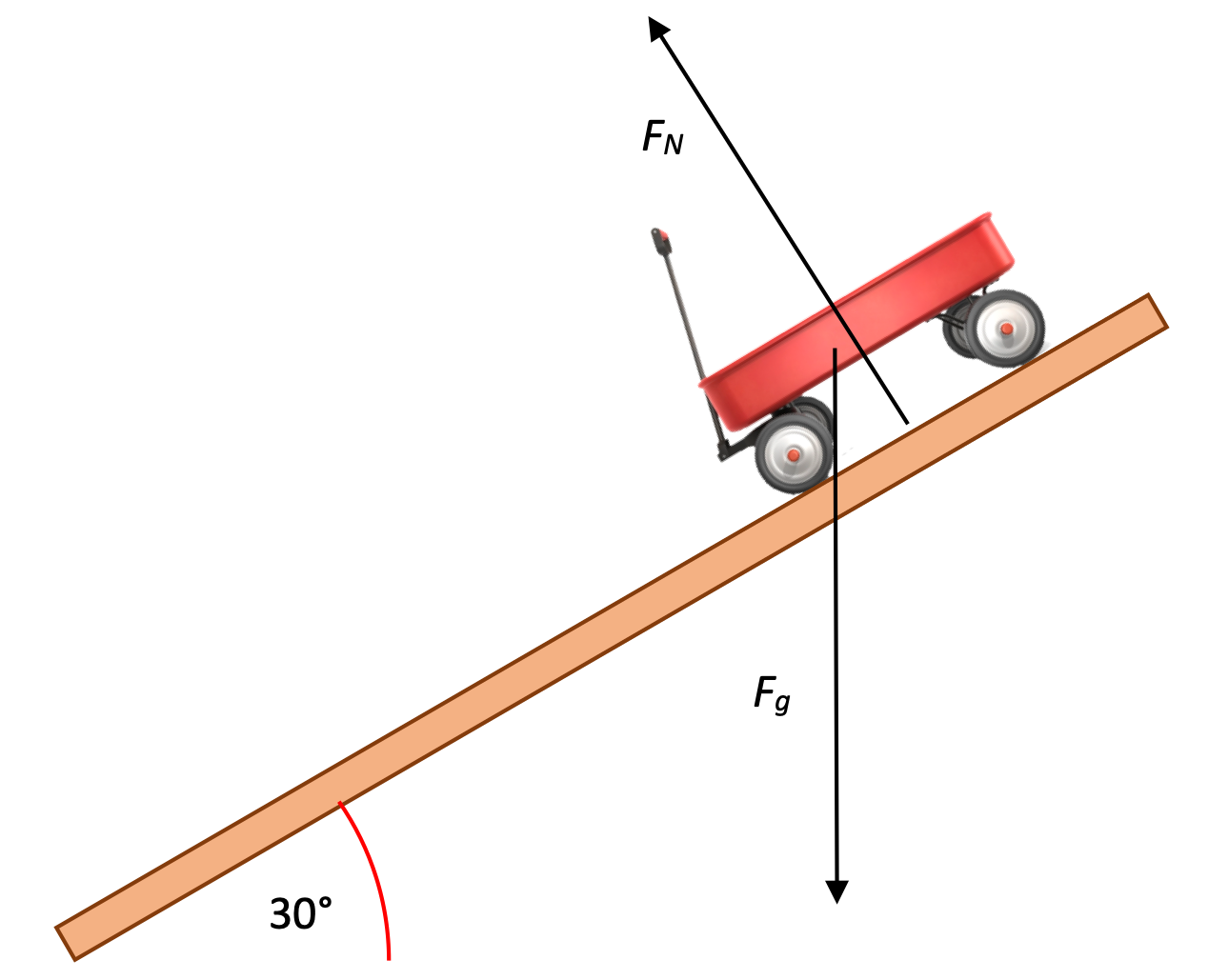
A classic type of physics problem involves an object moving along an inclined plane. These situations allow us to introduce some new problem-solving strategies.
In this diagram of a wagon about to roll down an inclined plane, there are two forces acting on the car: gravity and the normal force. Gravity, of course, points toward the center of the earth, and the normal force points perpendicular to the plane.
In the past, when there is a force at an angle, we've broken the force up into a horizontal x-component and a vertical y-component. We're going to do the same thing here, but we've actually got two ways we can consider this problem.
In one analysis, we might examine the problem using our standard x-y horizontal-vertical approach. The force of gravity would be downwards in the negative y-direction and we'd need to take that angled Normal force and break it up into components.
Another way to look at the problem would be to use an x-y axis system that is tilted so that the Normal force is pointed in the positive y direction. In this analysis, because the Force of gravity doesn't line up with our coordinate system, we have to break it up into components. This is the strategy that we're going to use to help us solve this problem.
Why tilt the axes? We could solve the problem using a standard orientation of the axes, but because the acceleration is down the ramp, it's easier to solve this problem using a tilted x-y coordinate system.
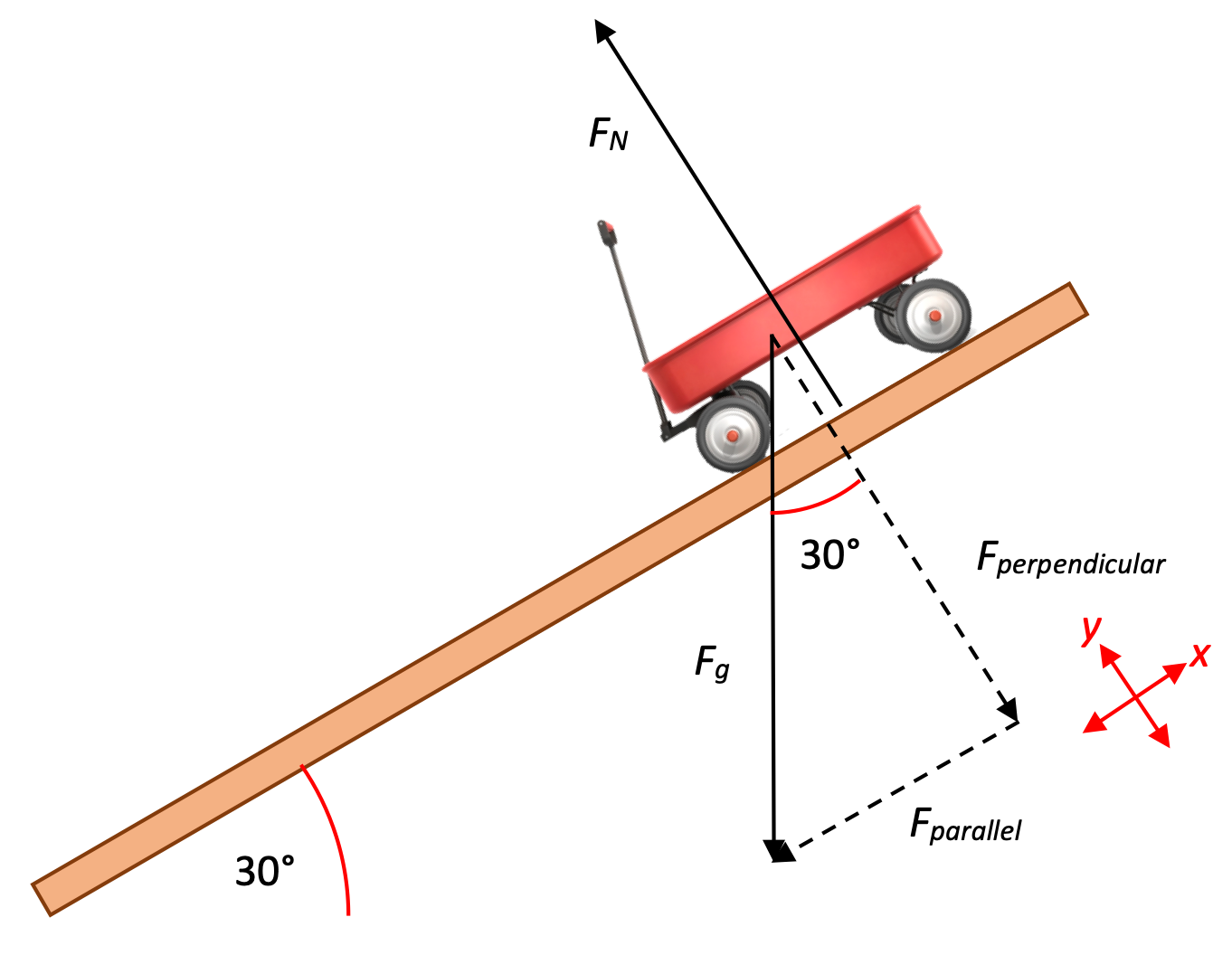
Because the incline causes our acceleration to be down in the inclined plane, we're going to "tilt" our analysis, with vectors that will more easily be able to help us solve the problem. As a result of these new tilted axes, we’ll need to split Fg up into x and y components. The Fgx , which acts parallel to the plane, is usually called F// ("F-parallel"). The Fgy , which acts perpendicular to the plane, is called F⊥ ("F-perpendicular").
We can now solve these inclined-plane problems in the same way that we've solved our other motion problems—applying Newton's Second Law, Fnet= ma in the x and y directions—being sure to use our new, tilted, x and y axes as a reference.
Downhill Skiing
A skier, beginning from rest, descends a slope that is essentially frictionless, and tilted at 60° below the horizontal. What is her acceleration? What is her speed after 6.0 s have passed?
Solution:
Because the skier is accelerating down the slope, we tilt our axes to that the x-axis runs along the length of the slope, and the y-axis is perpendicular to it.
Draw the free-body diagram for the skier, including both the force of gravity and the normal force.
Which of those two forces should we break up into components? According to our tilted axes, the Normal force lies along the y-axis, so we'll break up the Force of gravity into two components, the "force-parallel" and the "force-perpendicular."
Analyzing these using Newton's Second Law of Motion:
Once we know the skier's acceleration, and knowing that she begins her run from rest, we can calculate her speed 6.0 seconds later.
5.7. Pulleys
A pulley is a wheel mounted on an axle that allows tension in a string, rope, or cord to change direction. In the simple pulleys shown here, a downward pull applied at one end of the rope cause either a pull to the right or an upward pull to be exerted on the masses shown.
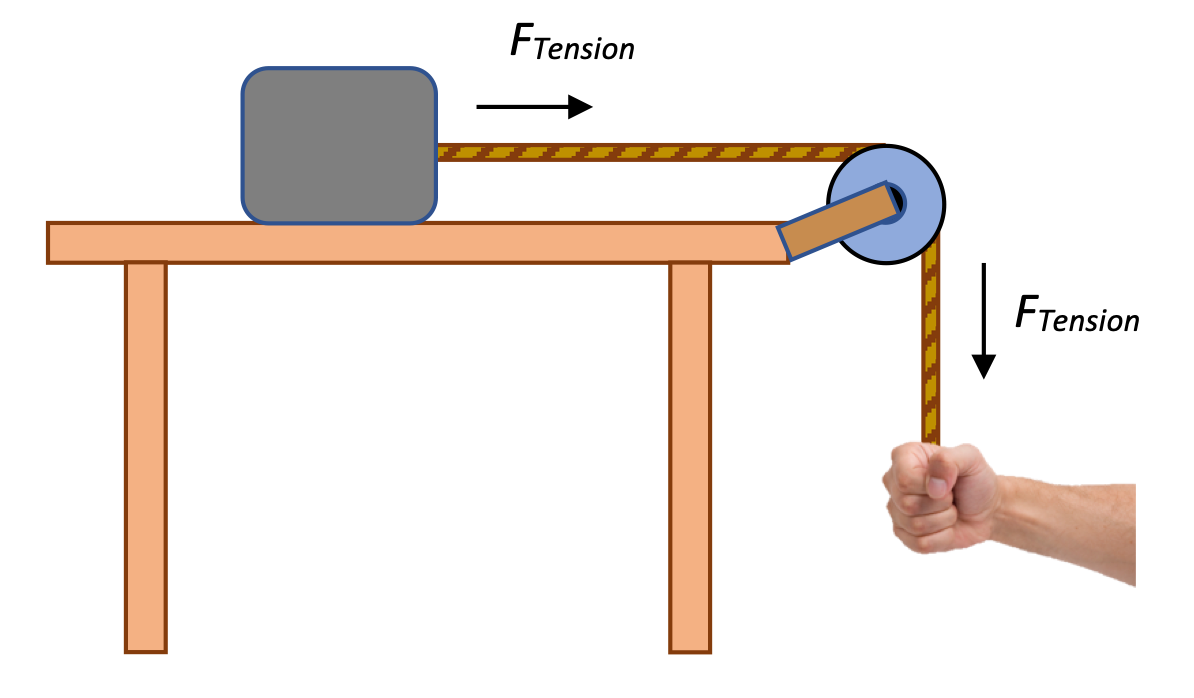
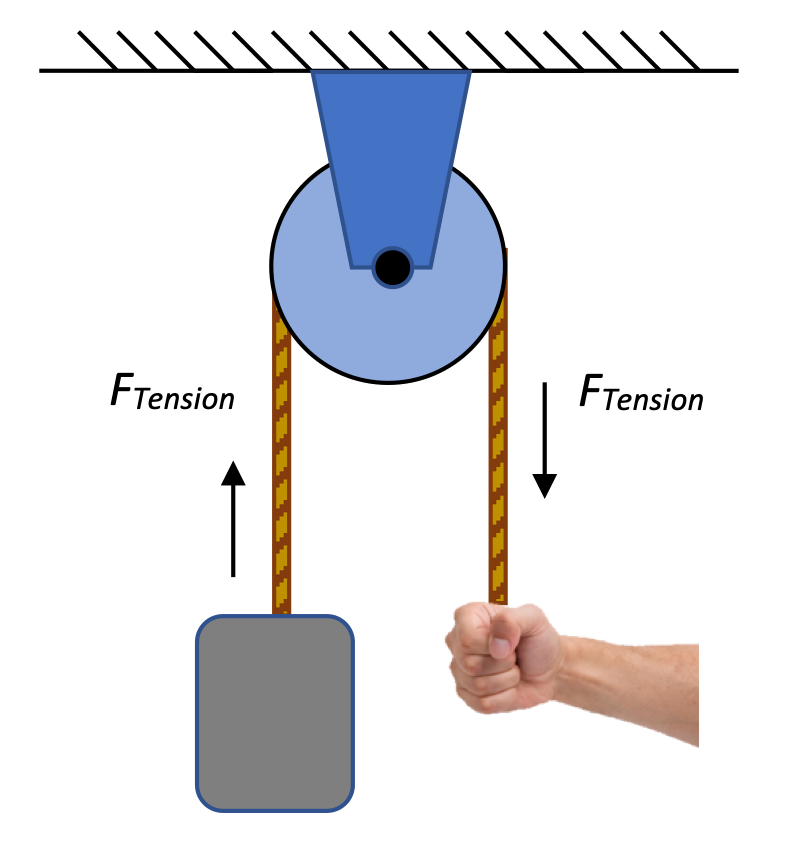
In these examples, the pulley is an "ideal" pulley, meaning that it is "massless and frictionless," a convenient simplification for introductory problems. Later in this course we'll look at pulleys that have non-negligible mass, meaning that some of the force we apply to the cord will have to go into turning the pulley.
For now, we know that if a hand pulls down with a force of 10.0 Newtons, then the tension in the cord will be 10.0 Newtons, and that tension will in turn be transmitted to the mass, which has a 10.0 Newton force applied to it via the cord.
Masses connected via a pulley
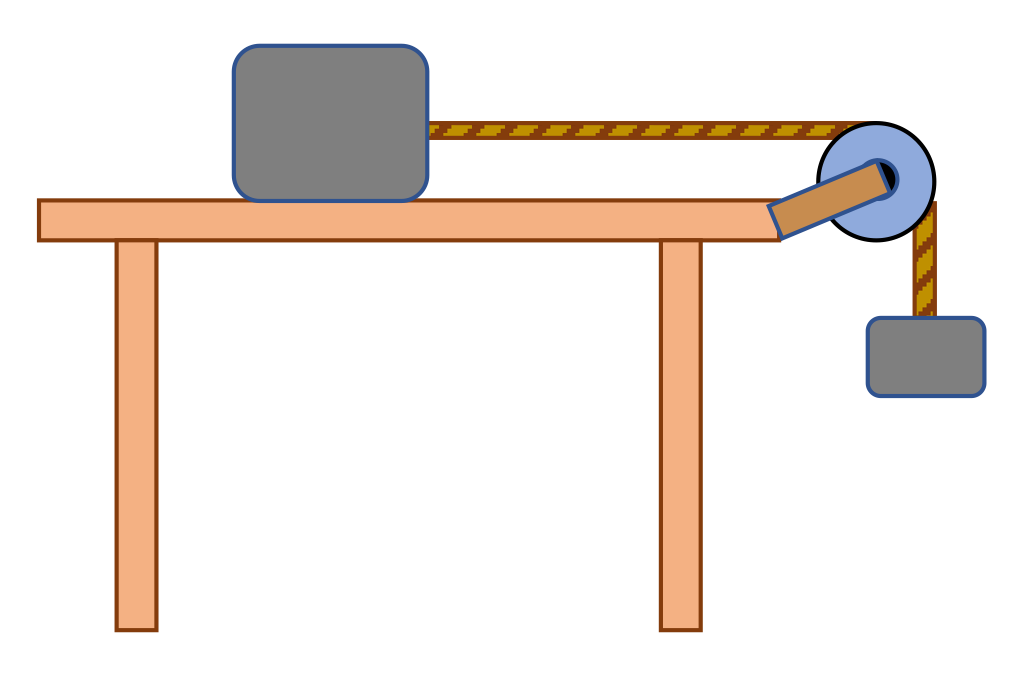
A 2.0 kilogram mass rests on a frictionless table, connected by a cord running over a pulley to a 1.0 kg mass hanging off the edge of the table. At first, the 2.0 kilogram is held in place so that it cannot move. Then it is released.
- What is the tension in the cord when the 2.0-kg mass is held in place.
- What is the tension in the cord once the 2.0-kg mass is released and the system starts to accelerate?
- What is the acceleration of the system?
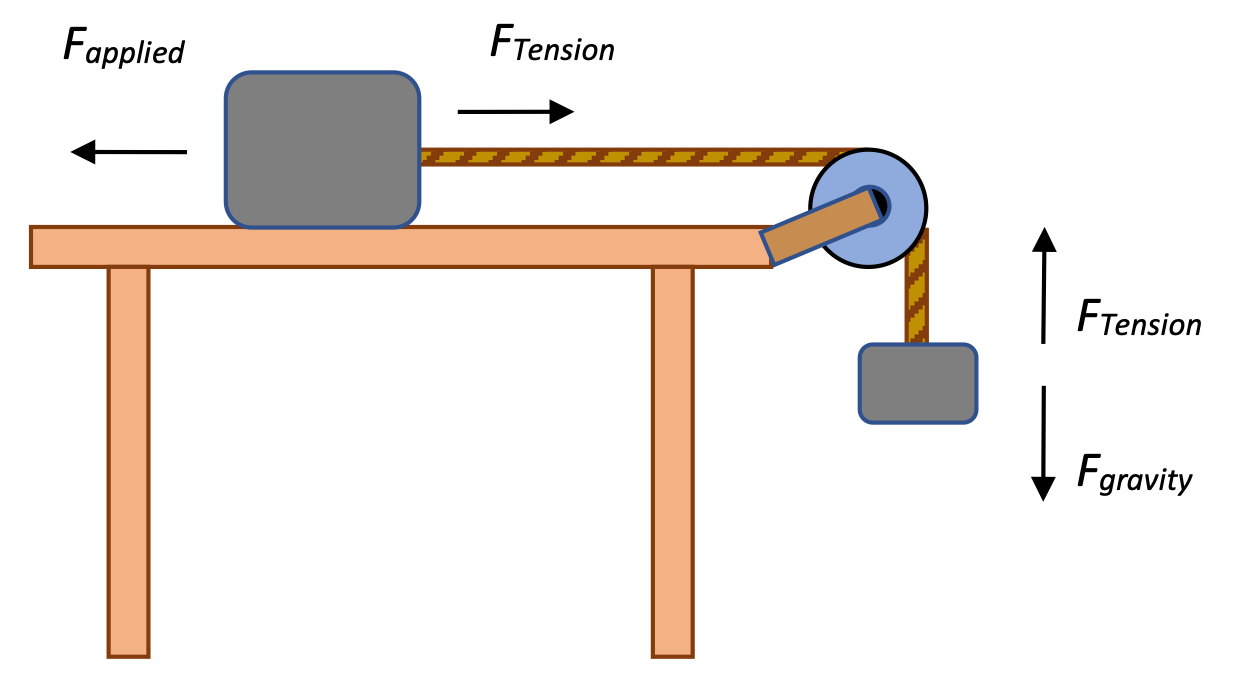There are two masses in this system, so to solve, we need to draw two free-body diagrams. (For the mass on the table, the vertical Fg and FN have been left off to simplify the diagram.) For the small mass hanging off the end of the table, the Force of gravity is balanced by the force of tension in the rope, and for the mass on the table (which is stationary), the Fapplied must equal the force of tension as well.To solve for that tension, it's easy to apply Fnet = ma to the mass hanging off the edge:
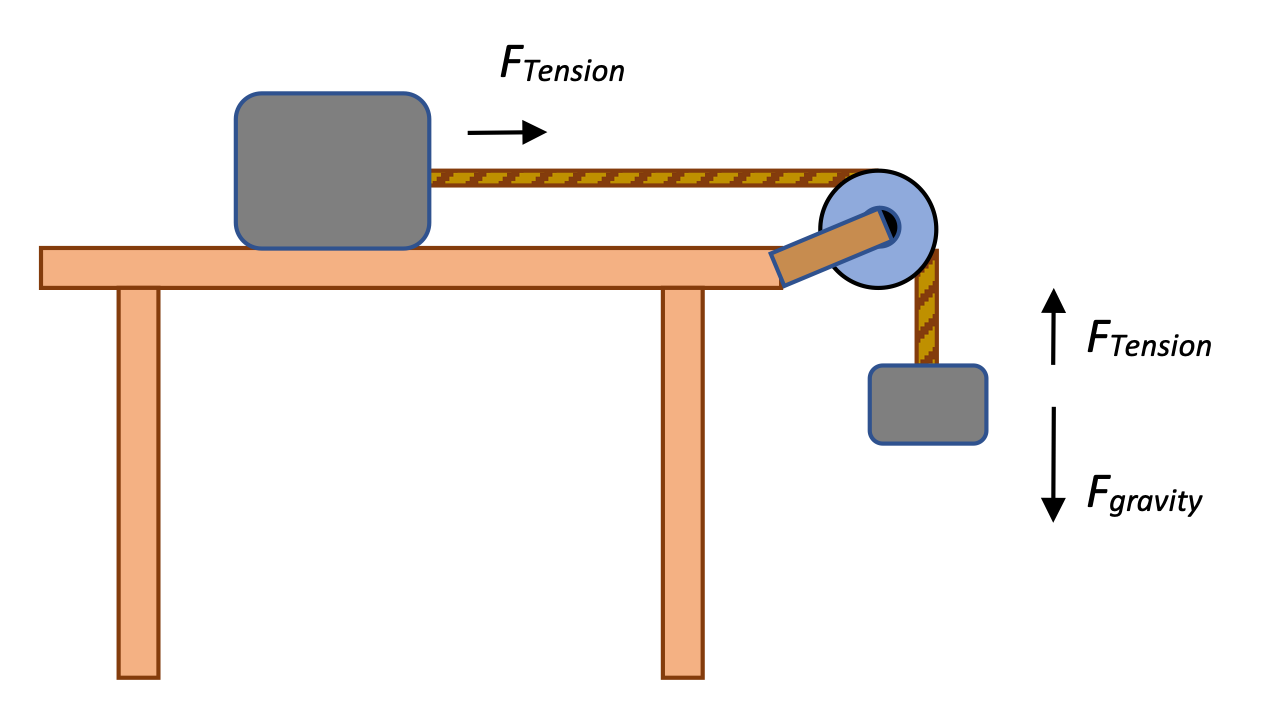Once the mass on the table is released, the entire system starts to accelerate due to the unopposed force of gravity. With two masses we can create two Fnet=ma analyses...
... and combine to solve for FTension:
It makes sense that this tension is a little less than it was before: the new Fnet for the mass on the side of the table is why it can start to accelerate downwards.
The Atwood Machine
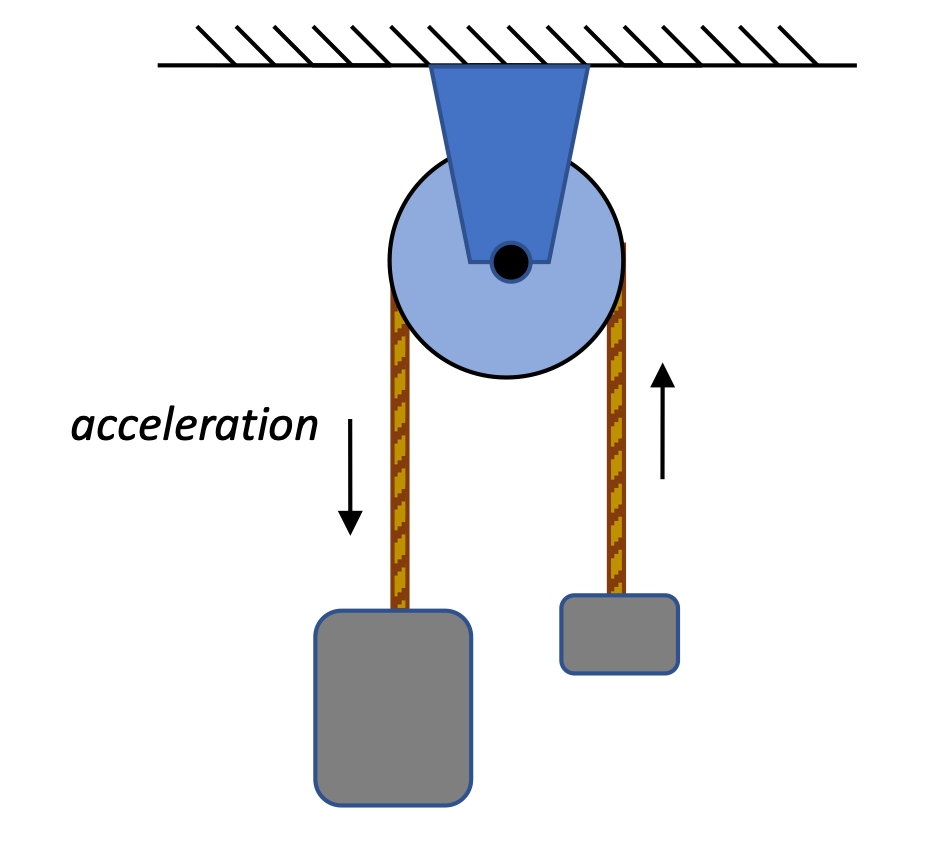
This diagram shows an "Atwood machine," with a larger mass m1 on the left and a smaller mass m2 on the right. The two masses are connected by a cord that runs over a light pulley. The masses are released from rest, and they start accelerating as shown. Find the acceleration (magnitude and direction) of the larger mass after the system is released, and determine the force of tension in the rope attached to the masses.
As with all Force-acceleration problems, we'll do free-body diagrams for each mass and use Fnet = ma to analyze each mass. With two equations, we should be able to solve for the two unknowns (acceleration and tension).
For the mass on the left:
For the mass on the right:
We have a problem with our equations, however. If we're going to be substituting and solving with these two equations, we need to make sure that the values we're solving for are the same. We've used a to indicate the acceleration of the masses, but they two masses are actually moving in two different directions. The two masses have the same magnitude of acceleration, but to indicate that they're moving in two different directions, we need to change one of the occasions.
One way to do this is simply to change the sign of one of the accelerations. For the left mass, we know it's going to be accelerating in the downward direction, so we can just manually change the a value to a negative one.
Another way to fix things is to call up for mass m2 positive, as we have already done, and call down mass m1 positive as well. In that case, the direction of the acceleration a is consistent with both sides.
Whichever way you choose to fix the equations, when we substitute and solve, we can calculate the acceleration of the masses.
We can substitute this expression back into a previous equation with FTension in it to solve.