
Chapter 13: Universal Gravitation
13.0. Overview
You know that whole story about where Newton "discovers" gravity when an apple falls on his head? That story gets so many things wrong, and worst of all, it doesn't even include one of the most interesting aspects of Newton's law of Universal Gravitation: at the time, in the late 1600s, the whole idea of the earth being able to exert a "force at a distance" on the moon was so ludicrous, that Newton wasn't sure if it should be included in a book along with his other scientific research.
There are some important things to be discussed here. Let's get started!
- Historical Context
- Newton's Law of Universal Gravitation
- Gravitational Potential Energy
- Orbits and Energy
- Gravity force as a function of radius
13.1. Historical Context
Isaac Newton (1642 - 1727) didn't "discover" gravity. The concept of "gravity" was developed over time by scientists in Greece, India, and Persia. Prior to Newton's consideration of the idea, Johannes Kepler (1561 - 1630) assisted Tycho Brahe in collecting large amounts of data on the motion of celestial bodies. This data, when analyzed, led to the development of Kepler's Three Laws of Motion, which describe quantitatively various aspects of orbiting bodies.

Galileo Galilei (1564 - 1642) performed a number of experiments in the lab to determine acceleration in free-fall, and made celestial observations by telescope, including discovering the "Galilean moons."

Newton, in part based on the information from previous scientist "stood on the shoulders of giants" to eventually arrive at his "Law of Universal Gravitation," outlined in his book the Philosophae Naturalis Principia Mathematica, published in July 5, 1687. (The Huntington Library holds several copies of the first edition, including two annotated by Newton.)

One of the fundamental questions that Newton was wrestling with was: If a centripetal force is required to keep something like the moon moving in a circle around the earth, what provides that force?
The story, almost certainly aprocryphal, is that an apple fell from a tree nearby, and the acceleration of that apple as it fell caused Newton to wonder if earth's gravity could extend out into space. The idea seemed absurd, but some initial calculations proved interesting.
The relationship between acceleration and distance
Identify (by looking up or calculating) each of the following:
- The acceleration of an apple at the surface of the earth (first determined by Galileo via experiments)
- The radius of the earth, in meters (first determined by Eratosthenes, 200 BCE)
- The radius of the earth-moon distance (first determined by Aristarchus, 270 BCE)
- The centripetal acceleration of the moon as it orbits the earth one every 27.3 days (can be calculated based on previous values)
One you've got these, set up a ratio between the acceleration of the apple and the acceleration of the moon.
Then look at the ratio of the distance of the moon to the distance of the apple.
What is the relationship between acceleration and distance for these values?
I give up. Who do you think I am, Isaac Newton?
- The acceleration of the apple at earth's surface is 9.8 m/s2.
- The radius of the earth is 6.38e6 m.
- The radius of the earth-moon distance is ~3.85e8 m.
- The centripetal acceleration of the moon as it orbits is ~2.73e−3m/s2.
It turns out that the apple's acceleration is ~3600 times that of the moon's acceleration. And it turns out that the moon is 60 times farther away from the center of the earth than the apple.
3600? 60? The moon is 60 times farther away, and has 1/602 of the acceleration of the moon.
Coincidence?
Even for Newton it was a little hard to believe that there was a connection between these two values, but it was intriguing...
13.2. Newton's Law of Universal Gravitation
Based on his work, Newton proposed that there was a relationship between these accelerations—and therefore these forces—that varied as the inverse-square of the distance between the bodies.
Newton's Law of Universal Gravitation
Every particle in the universe attracts every other particle with a force that is proportional to the product of their masses, and inversely proportional to the square of the distance between them. This force acts along a line joining the two particles.
Newton had determined that the inverse-square aspect of the distance between the particles was relevant, but he had no idea what the value of the gravitational constant G was. In order to determine G one would need to know the masses, distance, and gravitational force between two objects, and measurements sufficiently accurate didn't exist. The mass of of the earth itself had been estimated, but there were not realistic values that would allow for an accurate calculation to be made... until the English scientist Henry Cavendish used a mechanism devised by Charles Coulomb in France to identify the force between two given masses. Once this value was known, G could be calculated.
The universal gravitation constant
The universal gravitation constant G has a value
Because the mass of the earth had not been known previously, but could now be back-calculated using the Universal Law of Gravitation, Cavendish's experiment is sometimes called the "weighing the Earth" experiment.
Calculate the mass of the earth
Given the Law of Universal Gravitation, calculate the mass of the earth in kg.
An orbiting space shuttle

A 4.20e5 kg space shuttle is orbiting the earth in a circular path at a distance of 420 km above the earth's surface (rearth = 6.38e6 m).
- What is the radius of the space shuttle's orbit relative to the center of the earth?
- What is the acceleration due to earth's gravity acting on the space station?
- What is the acceleration due to earth's gravity acting on an astronaut here?
- What is the weight of the 60 kg astronaut here?
- What orbital velocity must the space station have to maintain this distance?
- For a satellite, what altitude above the surface of the earth should a satellite be placed so that it maintains a geosynchronous orbit (an orbit that matches the earth's rotation)?
- Same
- To solve this, we need to find a satellite speed that matches with the earth's rotational speed, and then place the satellite at the appropriate altitude where earth's gravity will keep it there.
Earth's rotational speed:From previous problem, we know that:
Converting angular velocity to linear velocity and solving for radius r:
This is the radius relative to the center of the earth. To get the altitude above the surface:
Elliptical orbits
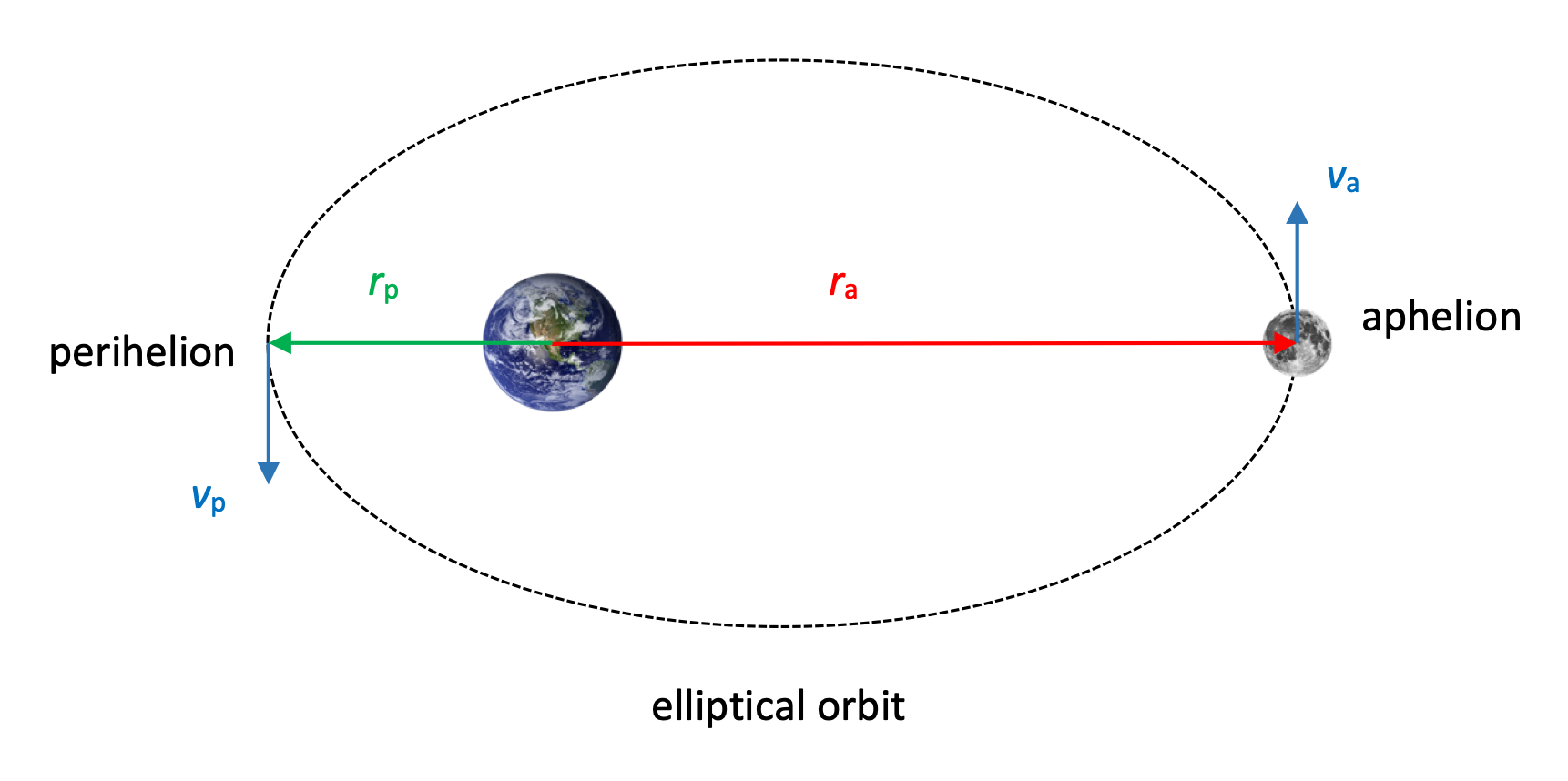
A satellite moves in an elliptical orbit about a large body. At aphelion, a distance ra, the satellite has a speed of va. Use conservation of angular momentum to calculate the satellite's speed at perihelion, where it has a distance rp from the body.
13.3. Gravitational Potential Energy
We've discussed gravitational potential energy before as mgh, which works as long as we're near the surface of the earth. If we start to move farther way from the earth, where the acceleration due to gravity is no longer g = 9.8 m/s2, we need to adjust our calculations.
13.3.1. Gravity force vs gravity field
Up to this point we've discussed gravity in terms of the the force that a mass feels due to the presence of another mass nearby.
A slightly different and better way to think of this is to consider the force that the mass feels in a gravity field.
A gravity field is produced by masses in a region of space. If we put any given mass in that field, it experiences a force due to that field.
13.3.2. Ug when ag != 9.8?
Recall that when a conservative force (like gravity) does Work on a mass, it causes a decrease in the potential energy of the system.

We have been able to solve problems using gravitation potential energy based on a change in mgh, where h referred to the height of a mass relative to some arbitrary zero position.
As we look at problems of greater scale, however, we'll see that the gravitational field g = 9.8 m/s2 is no longer constant over the range of the problem. As we look at greater distances, we'll see that we can no longer use Fg = mg. We'll have to use Newton's Law of Universal Gravitation, for which the force varies appreciably over the distances involved.
Thus, we'll need to develop a new potential energy function that is based on a varying field.
Potential Energy and Universal Gravitation
We can determine the change in potential energy for a mass moving through a gravity field as follows:
This value represents the gravitational potential energy of the system which includes both the mass of the earth and the mass of another object, planet, etc.
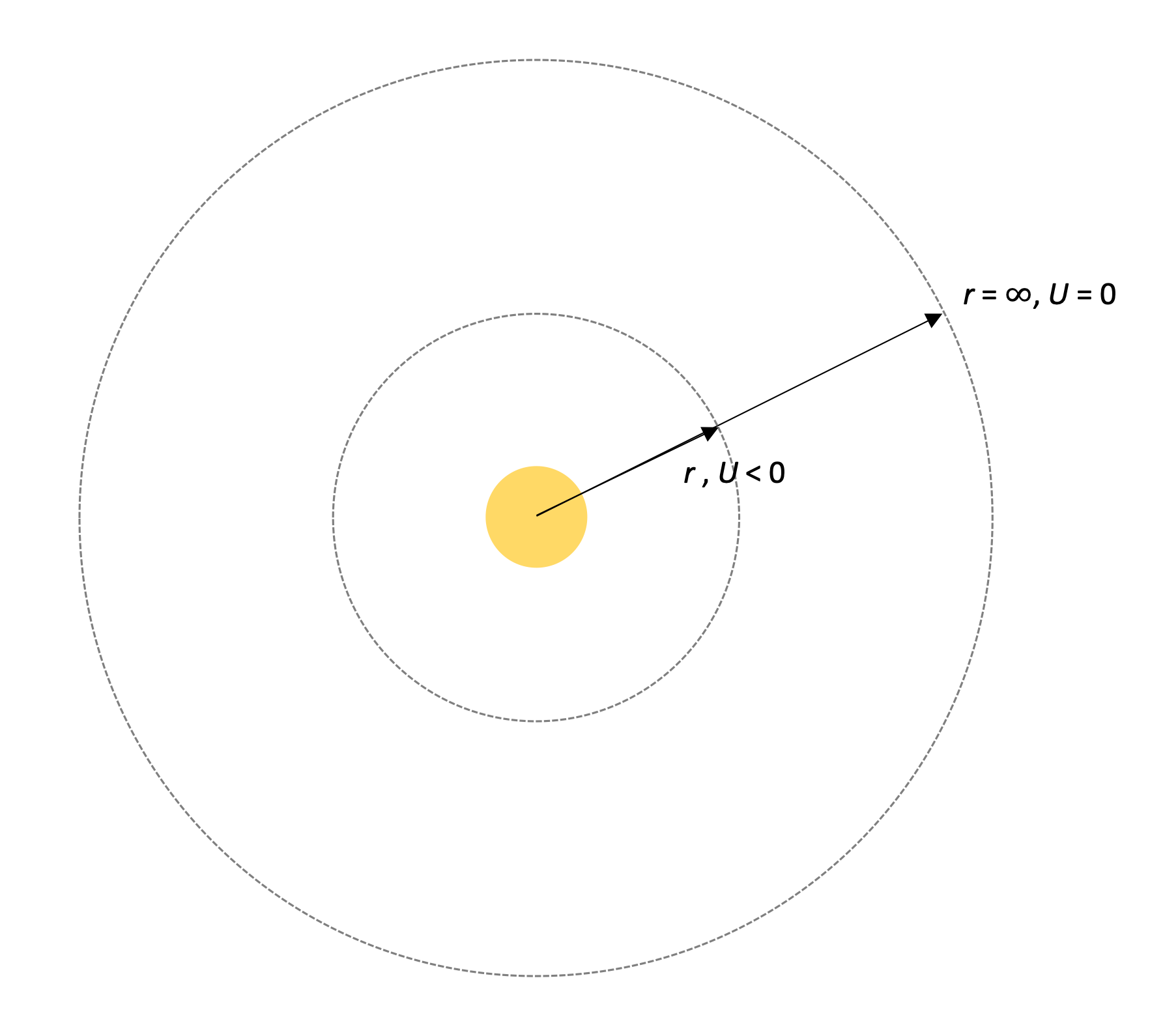
Thus, we can visualize the potential energy of a mass at a given radius from the center of the sun according to the following diagram. A mass infinitely far away from the sun, where it has zero potential energy in the system, loses potential energy as the sun's gravity pulls it closer, meaning the gravitational potential energy of the system starts to have a negative value.
A long way to fall
An apple is released from a height of 100,000 m above the surface of the earth. Use conservation of energy to determine how fast it is traveling right before it hits the surface of the earth. (Assume no air friction.)
Follow-up question: How fast would it be travelling if it had been falling with an acceleration of 9.8 m/s2 the entire time?
Let's use what we know about masses and energy to solve an "escape velocity" problem.
Escape Velocity
A rocket needs to launch itself from the surface of the earth with enough velocity that it completely escapes Earth's gravity field. What is this minimum escape velocity? Does it depend on the mass of the rocket?
In order for the rocket to "completely escape Earth's gravity field, it needs to travel infinitely far away from Earth, where the gravitational potential energy between it and the Earth is 0.
We'll need a lot of kinetic energy K to get there. What's the minimum amount of K needed? If we have too much Kinitial, we'll have excess K at the end, flying around at our final location infinitely far away. To get the minimum K, let's make sure we just make it to infinitely far away with zero K leftover. So:
13.3.3. Ug for multiple masses
We've developed the potential energy analysis where there are just two masses attracting each other. If another mass is introduced to the system, the potential energy is simply the sum of the individual potential energies between each pair of masses.
13.4. Orbits and Energy
The moon orbits the earth, the planets in our solar system orbit the sun... orbital motion is something we're all familiar with.
A satellite is a general term used for any body that is in orbit around another. For our introductory examples here we're going to consider a much larger mass that is effectively stationary, with a smaller mass—the satellite—in orbit around it. (In reality, both bodies are in orbit around the center-of-mass of the system, but in many cases, our simplification works well enough.)
13.4.1. Kepler's Laws
Kepler was able to arrive at some interesting mathematical conclusions based on the data collected by Tycho Brahe. Those conclusions are summarized in Kepler's Three Laws (which you don't really need to know for this class):
- All planets move in elliptical orbits, with the Sun at one of the focal points.
- The radius vector drawn from the Sun to a planet sweeps out equal areas in equal time intervals.
- For two different planets orbiting the sun at different distances,
If you're interested in learning more about Kepler and his place in scientific history, this Mechanical Universe video is excellent.
13.4.2. Energy of a Planet-Satellite System
How can we determine the total mechanical energy for a planet-satellite system?
For any two bodies at a given point in time:
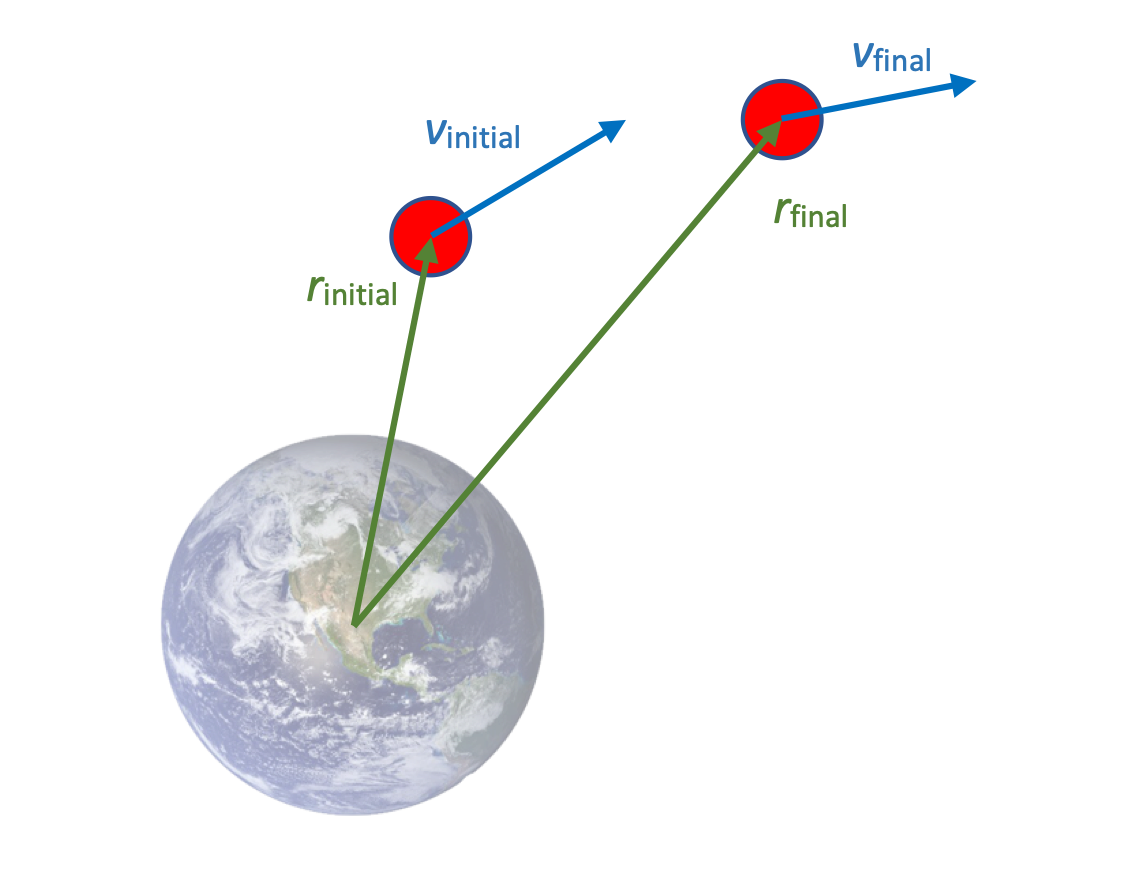
The total energy of the system might be positive, negative, or even 0, depending on the proximity of the two bodies and the velocity of the satellite.
In thes example here, the red satellite has an initial K and the system has some U when the satellite is closer to the earth. As the satellite moves away from the earth, the potential energy of the system increases, and the kinetic energy of the satellite decreases. The total mechanical energy of the system remains constant.
Let's see what happens when we consider the energy of a "bound," circular system, in which the centripetal force that keeps the satellite orbiting is provided by gravity.
Energy of a bound, circular orbit
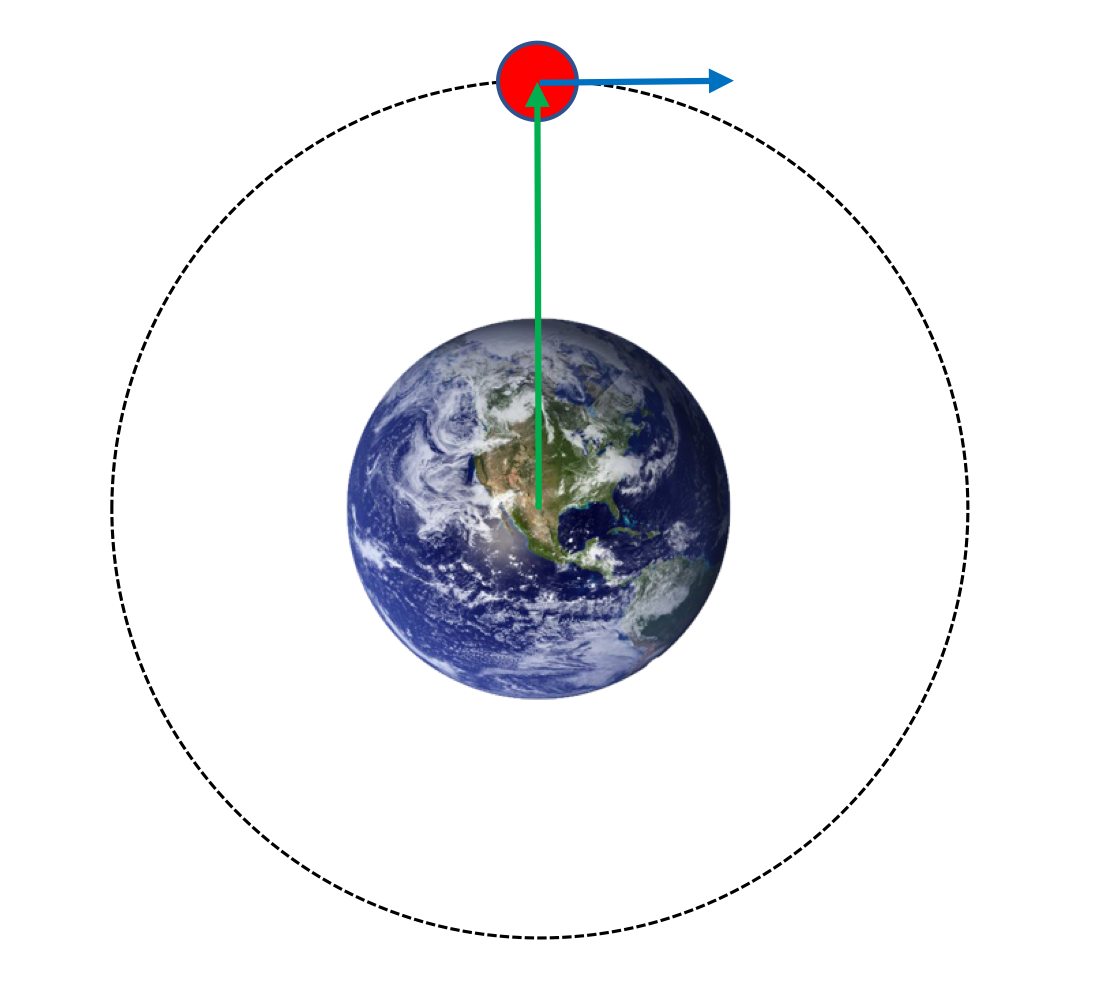
For a satellite orbiting a larger body in a circular path, we can easily calculate the total energy of the system.
Using a force analysis for the circular motion:
Continuing with what we know about total mechanical energy as developed above,
Based on this analysis, we can see that the total energy for a system where a satellite is orbiting a mass is a negative value.
This isn't an issue, because of course the gravitational potential energy for any two masses that are less than infinitely far apart is negative, and in this orbital case, so negative that it exceeds the positive kinetic energy of the system.