
Chapter 11: Angular Momentum
Topics covered in this chapter
After completing this unit you will:
- be able to consider a rolling object in terms of its translational and rotational motion
- be able to draw free-body diagrams for a round object rolling down a ramp and up a ramp
- be able to use a position vector r and a momentum vector p to identify an angular momentum L for a mass moving through space
- be able to demonstrate magnitude and direction for angular momentum vectors using a Right-Hand Rule analysis
- be able to use moment of inertia I and angular velocity to identify the angular momentum for a rotating body
- be able to identify the relationship between torque τ and angular momentum L
- be able to use Conservation of Angular Momentum to analyze rotation under conditions of varying radius
- recognize that Conservation of Energy, Conservation of Linear Momentum, and Conservation of Angular Momentum are three different conservation laws that describe three different aspects of masses and their motion
11.0. Overview
This section covers two important topics that are related to rotational motion: rolling objects, and the fascinating topic of angular momentum.
Let's get started!
11.1. Rolling Objects
We've already spent a little time looking objects that are rotating about an "axis of rotation," and up to this point, that axis has been fixed. A "rolling object" is one in which an object rotates as it moves, with friction between a surface and the object applying a torque that causes it to rotate.
11.1.1. Motion of the center-of-mass
When a round object rolls along a flat surface, in the course of a single revolution a point on the outer edge of the object rotates 2π radians, and the object "translates" a distance of 2πr meters.
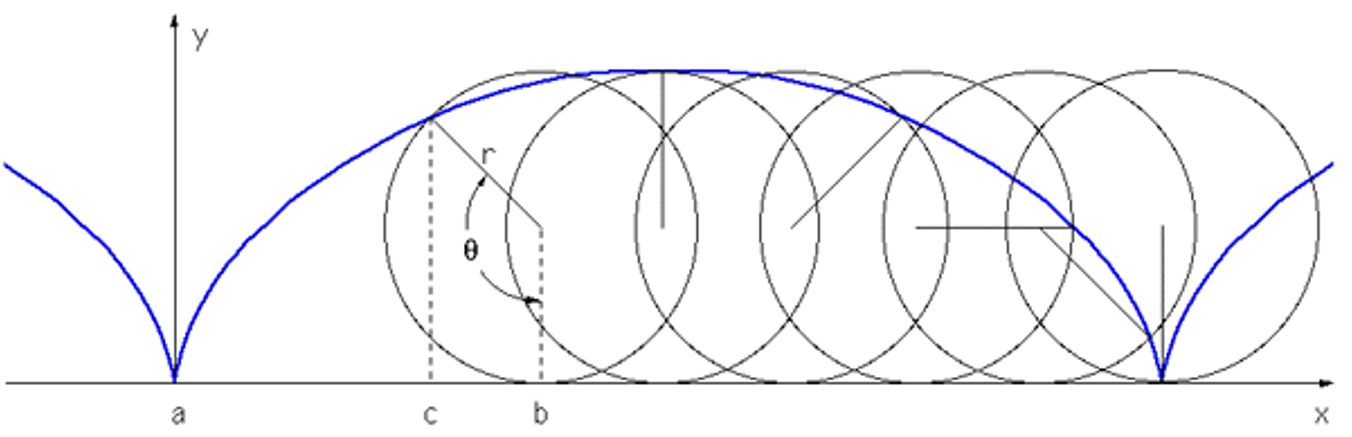
We can use this relationship to derive some interesting equations.
Equations of motion for a rolling object
The distance a point travels around the circle, s = rθ, and the distance traveled by the center-of-mass of the object, xcm are the same.
Continuing this relationship:
These equations look similar to the ones we've developed before for a fixed-axis rotation, don't they? But they are different:
- s = rθ refers to the tangential displacement around the radius of the object, while xcm = rθ refers to the translational distance the rolling object moves.
- v = rω refers to the tangential velocity of a point as it rotates around the axis, while vcm = rω refers to the translational velocity of the rolling object as it rolls along.
- a = rα refers to the tangential acceleration of a point as it rotates around the axis, while acm = rα refers to the translational acceleration of the rolling object as it moves.
We'll find these relationships very useful in solving a variety of rolling-object problems.
11.1.2. Total Kinetic Energy for a rolling object
We won't do the analysis here, but it can be shown that the total kinetic energy for a rolling object can be calculated as the sum of its translational and rotational kinetic energies.
Kinetic energy for a rolling object
The total K energy of an object undergoing rolling motion is the sum of the rotational K energy about the center of mass, and the translational K energy of the center of mass.
Rolling down an inclined plane - energy analysis
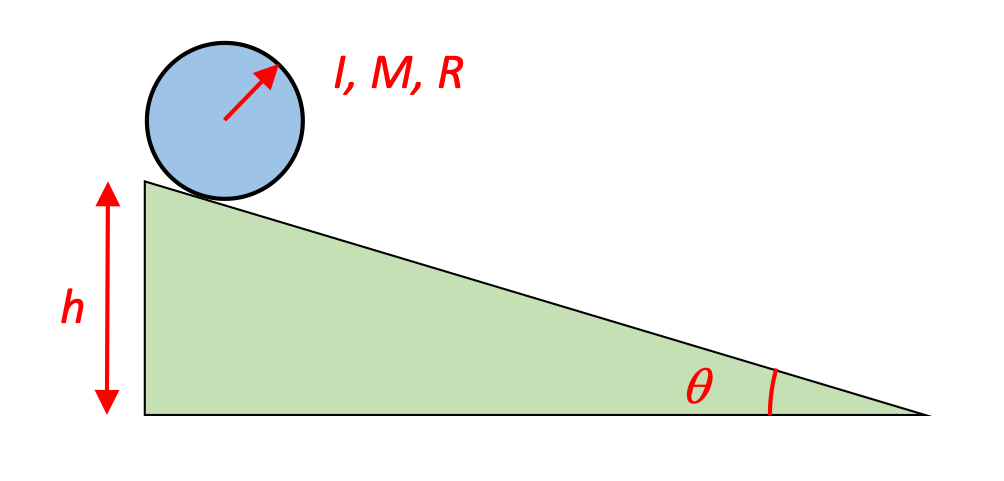
Find the speed at the bottom of an inclined plane for a rolling sphere (see diagram) using energy concepts.
We've been instructed to use energy concepts, so let's define the top of the ramp as our initial position and the bottom of the ramp as our final position. Then identify the energies that are present at each of those positions.
We've been told that this is a sphere that's rolling, so we can use the known moment-of-inertia for a sphere:
So this is the velocity of the sphere at the bottom of the ramp. Note that neither the mass nor the radius of the rolling sphere factor into the final velocity of the sphere at the bottom. Interesting!
Assuming that the sphere is accelerating constantly (and it is, as we'll soon see), we can use kinematics to identify its acceleration as it rolls.
Rolling down an inclined plane - force analysis

Find the acceleration, and speed at the bottom, of a sphere rolling down an inclined plane as shown, using a Force analysis.
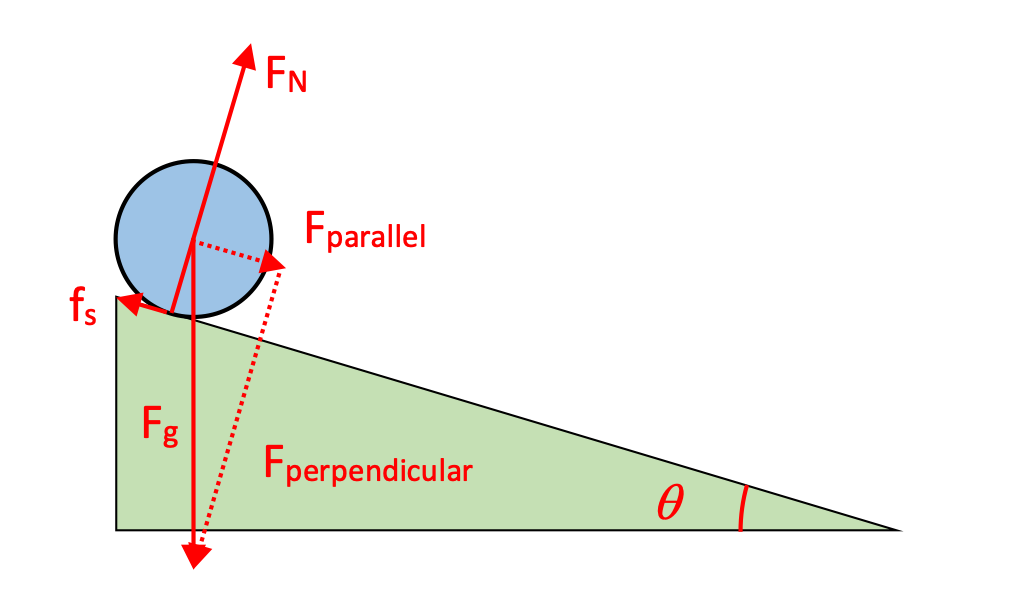
This problem is asking the same questions as the previous one, but we're using a force-and-torque analysis instead of energy. That, of course, requires a free-body diagram for the rolling object, shown here.
Because the ball is accelerating down the ramp, we choose to tilt our axes, so positive-x is down the ramp. Forces acting in that direction include the force-parallel due to gravity and the force of friction between the ball and the ramp, which both inhibits the motion of the ball down the ramp and acts as a torque around the axis of rotation, causing the ball to start to rotate.
You might be tempted to substitute in fstatic = μFNormal, but recall that μstatic represents a "maximum stickiness" that is possible; the fstatic in the problem at this point is not necessarily that maximum value. At this point we don't know what that friction force actually is, nor what the acceleration of the sphere is. We'll need to turn to another strategy to get additional information.
Substituting this into the previous equation:
This matches the result from our energy-based analysis above.
From here, it's simple enough to use this acceleration value with kinematics to identify the velocity of the ball at the bottom of the ramp, a result which also matches that arrived at above.
Rolling down an inclined plane - friction analysis
Based on the previous analysis, what is the minimum μstatic necessary for the object to roll? What happens if the μstatic is less than that minimum value?

For a given ramp angle θ a certain amount of "stickiness" is required for the sphere to be able to roll. Let's calculate exactly how much.
Using information from our calculations above:
If the actual μstatic is smaller than this value, the sphere will be slipping as it rolls, losing some energy to frictional heat losses. As a result, it will have less total K by the time it reaches the bottom of the ramp. Its rotational speed will be less (why? Do a τ = Iα analysis!) but its translational speed will be greater (why? Do an Fnet = ma analysis!).
Which one wins?
A hoop, a ball, and a solid cylinder are all released from the top of a ramp at the same time so that they roll down. Which one reaches the bottom first? Does it depend on the mass of the objects? Does it depend on their relative radii?
One strategy for solving this problem consists of repeating the acceleration calculation that we just performed on the sphere, applying that analysis to the hoop (Ihoop = MR2), and the solid cylinder (Icylinder = (1/2) MR2).
We've already determined in our analysis of the sphere above that the mass and the radius of the rolling object are not a factor in its acceleration.
This video provides some experimental evidence.
11.2. Angular Momentum
We've already described the linear momentum of an object, a vector quantity based on its mass m and its vector velocity v.
In an isolated system (no external forces applied from outside), linear momentum is "conserved": the total linear momentum remains the same over time.
The rotational analog to linear momentum is angular momentum, which is also a conserved quantity.
Definition of Angular Momentum
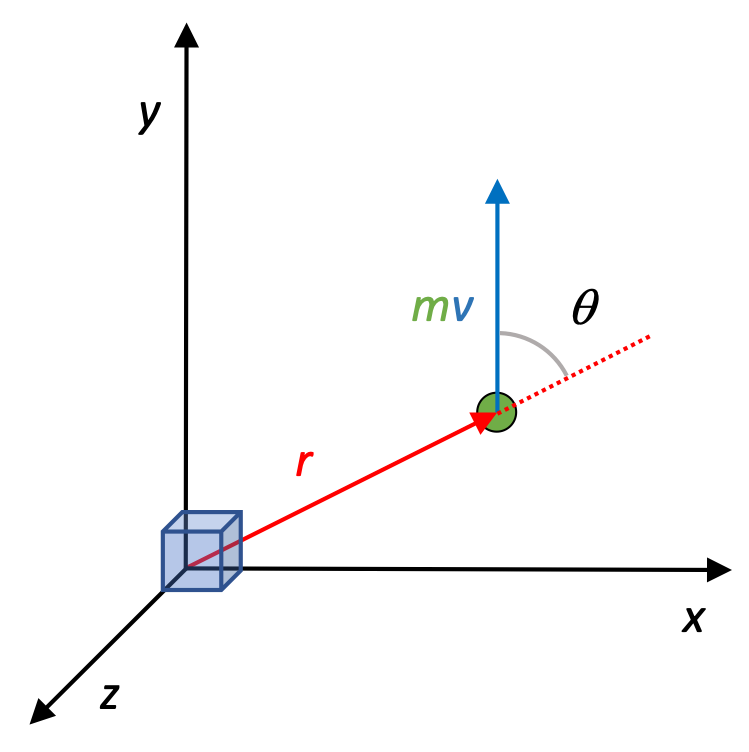
A particle of mass m, traveling with a velocity v, has an angular momentum relative to any given point in space.
We've used the word "angular" to refer to rotational quantities, but it's important to understand that even a mass traveling in a straight line has an angular momentum relative a a given point in space.
Under what circumstances is the angular momentum of a particle 0?
Under what circumstances is the angular momentum of a particle rmv?
It may take a little time to develop an intuitive understanding of angular momentum. To help us become more familiar with the idea, let's solve a problem.
Angular momentum of a circling particle
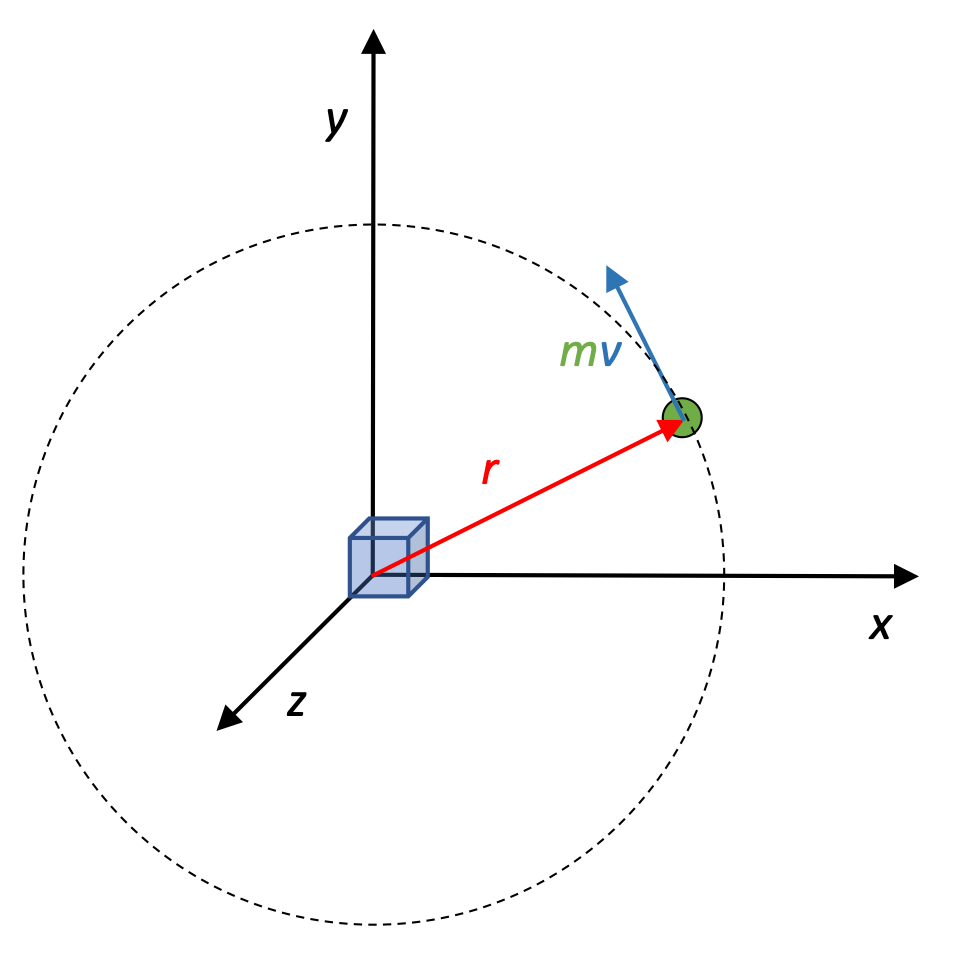
A particle with mass m moves in a counterclockwise circle, with a speed v in a counterclockwise circle with radius r, centered about the origin.
- Find the magnitude and direction of the particle's angular momentum L relative to the origin.
- Find L in terms of angular velocity ω.
- The magnitude of the angular momentum can be calculated using the values given in the problem:
The direction of the angular momentum, using the coordinate system shown in the diagram above, is determined using the Right Hand Rule. That direction is "counterclockwise" as we view the situation, but a more precise answer would be "out of the page" or "in the positive-z direction."
- First find the angular velocity of the particle, then use that relationship to calculate L.
Notice that this result is a rotational analog of the relationship p = mv.
Angular momentum of a particle moving in a straight line
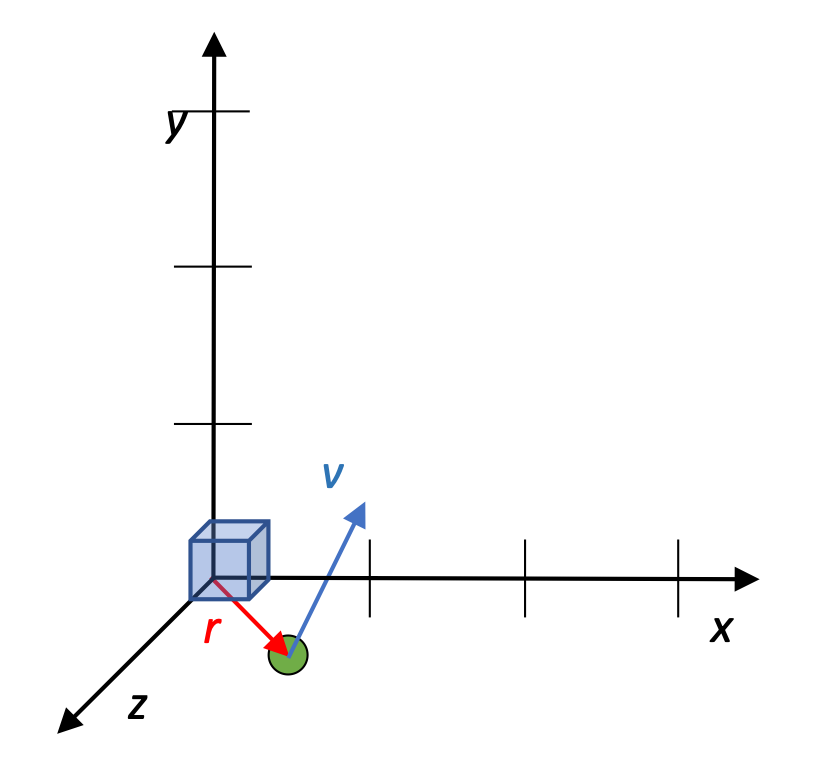
What is the magnitude and direction of angular momentum L relative to the origin for a 2-kg particle traveling at a constant (1i + 2j) m/s at the instant it is at (1i - 1j) m?
What is its angular momentum 3 seconds later?
The angular momentum is originally calculated as follows:
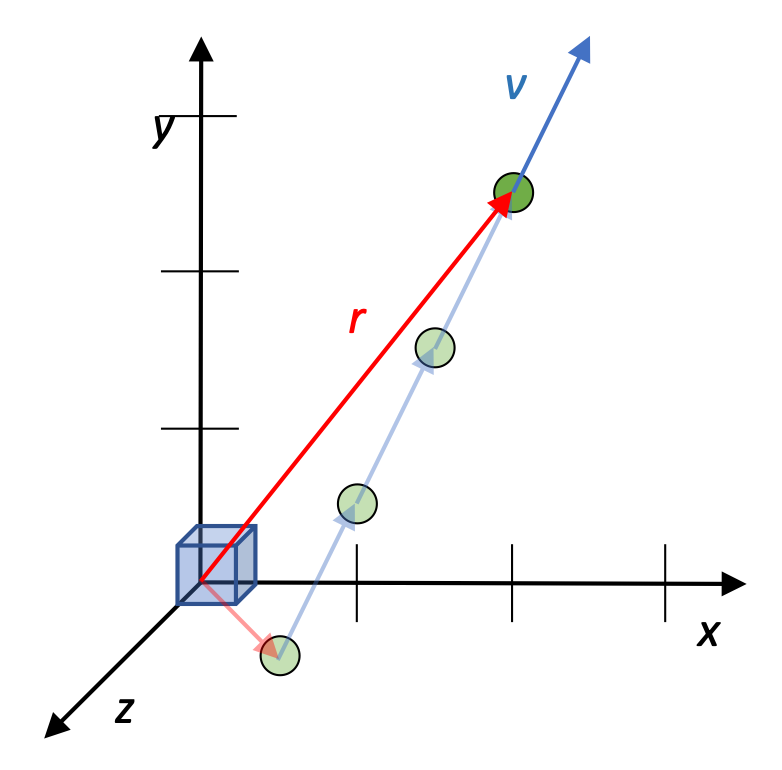
What about three seconds later? Let's first identify where the particle is three seconds later...
... and then calculate the "new" angular momentum L.
Note that this value is the same as the value we had before. The angular momentum of the particle relative to the origin remains unchanged.
This is similar to the way the linear momentum of a moving particle remains unchanged... unless, of course, a net force acts on it, providing an impulse to change its momentum.
11.2.1. Relationship between Torque and angular momentum
We've already seen that a torque causes a mass with a moment of inertia I to have an angular acceleration α.
We've also seen that, in a linear situation, a Force causes a change in linear momentum.
Is there an angular analog to that linear relationship? How does Torque affect the angular momentum of a mass?
Torque and angular momentum
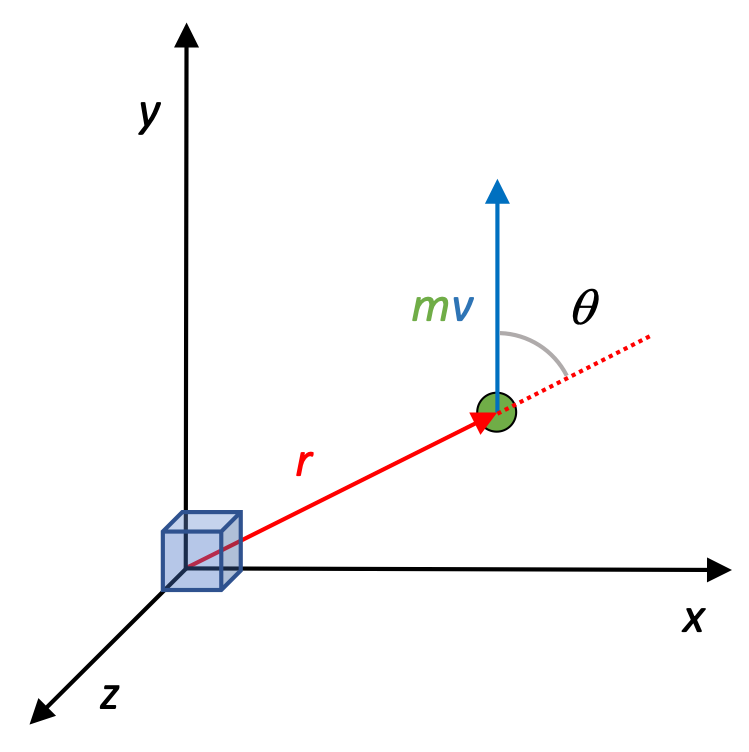
Let's see what relationships we can develop between Torque and angular momentum. Looking at Torque first:
And let's look at angular momentum, and in particular what happens when we take the time-derivative of angular momentum:
Substituting in:
This equation is analogous to the linear relationship between an external Force and change in momentum.
11.2.2. Angular momentum for a larger body
We've already identified the angular momentum for a single particle traveling in circle:
If we have a collection of particles traveling in a circle, their total angular momentum can be easily calculated.
Angular momentum for an extended body rotating

A single mass mi rotating about an axis of rotation has an angular momentum about that axis that is easily calculated as rmv.
For an extended body with a number of masses mi:
11.2.3. Ways of analyzing angular momentum
At this point we've talked about angular momentum from a number of perspectives. If you're asked to consider a problem in terms of angular momentum, you'll probably be using at least one of these relationships:
Angular momentum of a disk
A uniform disk of radius 25 cm and mass 5.0 kg rotates about a z-axis through its center. What is the angular momentum of the disk when its angular velocity is +2.0 rad/s?
Using the angular momentum for a disk:
Multi-component rod accelerated by gravity
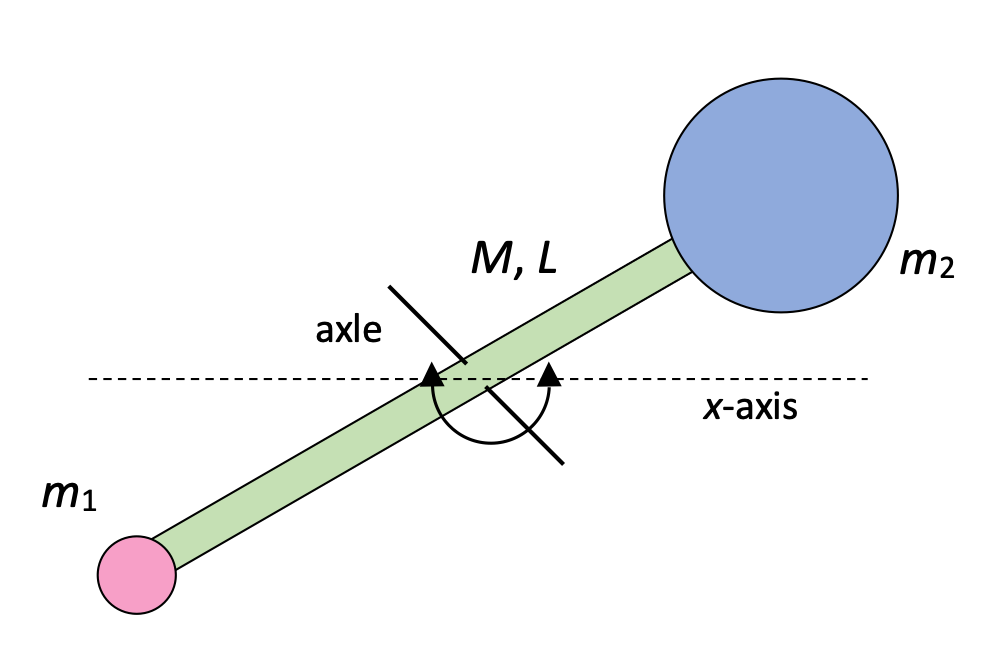
The rotating rod here consists of three components attached to each other: a long, thin rod of mass M and length L, and two other masses, m1 < m2, attached to its endpoints. The rod has an axle through its center around which it can rotate. The rod is held in the position shown, released from rest, and gravity causes the rod to begin rotating in a clockwise direction about the rod's midpoint.
- Find L as a function of ω.
- Find angular acceleration α when the rod reaches a horizontal position.
- To find L as a function of ω we simply need to identify the moment of inertia of the system, because
Let's do that then:
Thus, we end up with:
- To get the angular acceleration, let's use a torque analysis:
Pulley, masses, accelerating
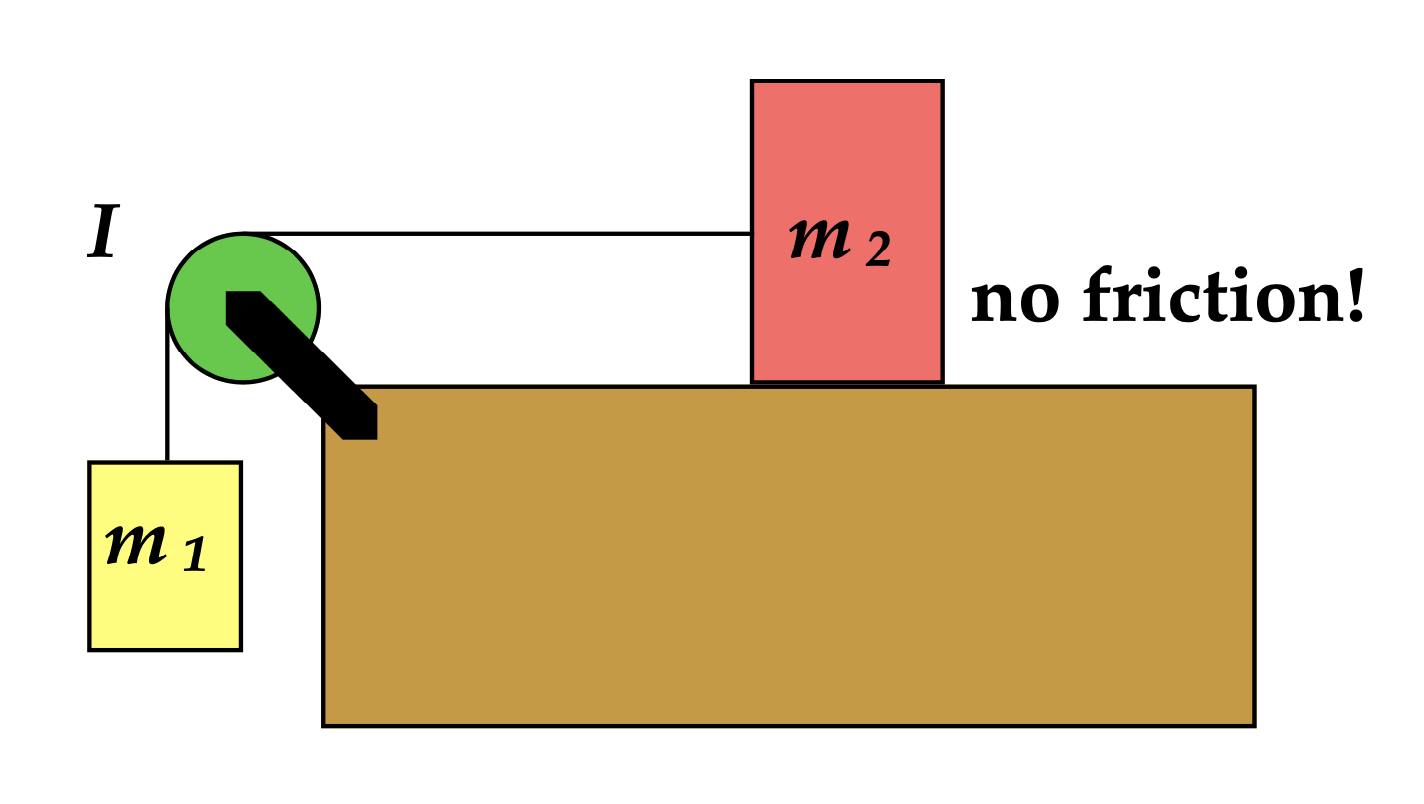
Two masses are connected as shown here. Find the acceleration of the system using angular momentum.
11.3. Conservation of Angular Momentum
For any system, even one consisting of multiple masses, if there is no external torque acting on the system that its angular momentum will remain constant.
The total angular momentum at one time will be the same as the total angular momentum at another time, even if particles are changing their positions or velocities.
Conservation of Angular Momentum
The total angular momentum of a system is constant in both magnitude and direction if the net external torque acting on the system is zero, that is, if the system is isolated.
For a large system of particles:
For a system rotating about a fixed axis:
... even if the distribution of the masses in the system changes.
11.3.1. Examples
There are lots of examples of conservation of angular momentum. This video introduces a few.
Here are a couple of more.
11.3.2. Angular Relationships
11.3.3. Problems
Star collapse
A star with a radius of 1e4 km rotates about its own axis with a period of 30 days. It then undergoes a supernova explosion and collapses into a neutron star with the same mass, but a radius of only 3km. What is its approximate period of rotation after the collapse?
Walking on a merry-go-round
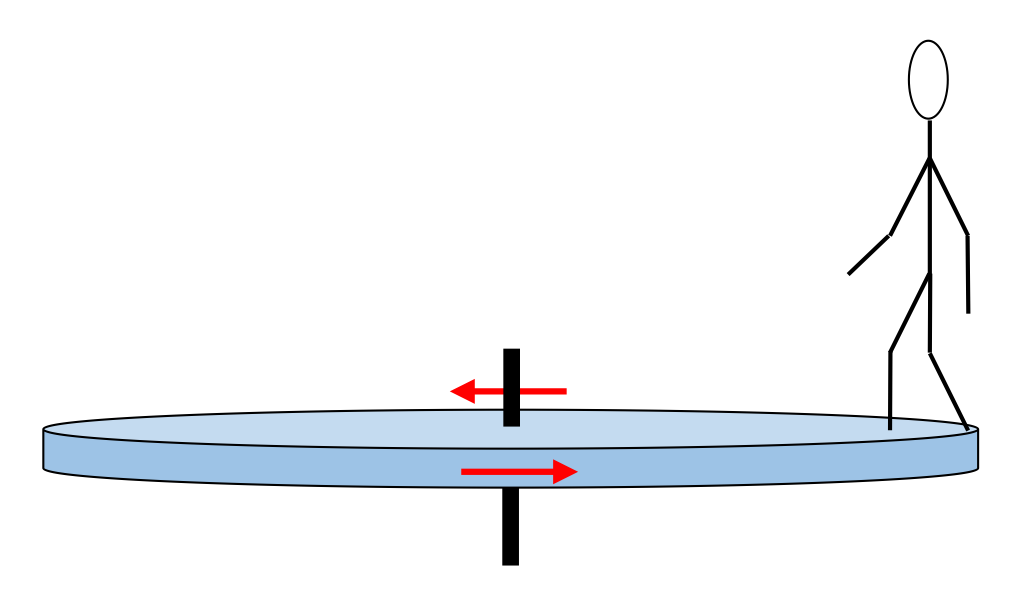
A horizontal platform (disk-shaped) rotates in a horizontal plane about a frictionless vertical axle. The platform has mass 100 kg and a radius R = 2.0 m. A student of mass 60 kg stands at the edge of the spinning platform and walks slowly from the rim toward the center. If ω0 = 2.0 rad/s when the student is standing at the edge of the platform:
- What is the moment of inertia of the combined disk-student system when the student is standing at the edge of the platform?
- Calculate ω when the student is 0.50 m from the center.
- Calculate the initial and final rotational energies of the system.
- Are the energies from your last answer the same? If not, what accounts for the difference?
- Itotal = Idisk + Istudent
Itotal = (1/2)(100)(2)2 + (60)(2)2 = 440 kg m2 - ω = 4.09 rad/s
- Ki = 880 J, Kf = 1.8e3 J.
- As student walks across the platform, they are doing work on the system, which adds energy.
Follow-up question: If the student started closer to the middle of the platform and walked to the edge, would they still be doing work on the system, adding energy to it? Or would the system be doing work on them, and thus "losing" mechanical energy?
Object colliding with a cylinder
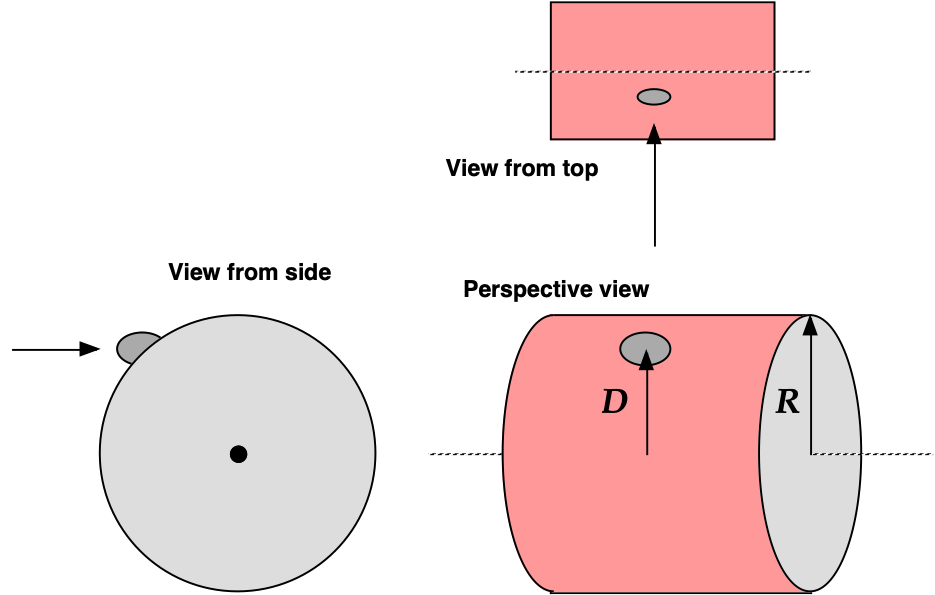
A projectile of mass m and velocity v0 is fired at a solid cylinder of mass M and radius R. The cylinder is initially at rest, and mounted on a fixed horizontal axle that runs through its center of mass. The line of motion of the projectile is perpendicular to the axle, and at a distance D < R from the center.
- Find the angular speed of the system after the projectile strikes and adheres to the surface of the cylinder.
- Is mechanical energy conserved in this example? Give quantitative evidence to support your answer.
11.4. Precession
When it comes to conservation of angular momentum, one of the most interesting aspects that one can easily observe is that of precession.
Take a look at this video which does a nice job of demonstrating the vectors graphically.